DSCF2525

X kolei obliczamy P(A), P(B), P(C):

PU)

ilość części grup uczniów, którzy zwiedzili dział A ilość wszystkich części

Analogicznie: P(B)^ \ i P(C)~\. Ponieważ

PM I#)

P(B),

P(A\C)~P(A),    P(B\A)<=* P(B\C)

P(C\A)~P(C\B)~P(C),

to zdarzenia są parami niezależne (definicja 4.5.3).

Czy te zdarzenia są niezależne zespołowo? (W tym przypadku niezależność zespołowa I jest równoważna niezależności parami i trójkami). Pytamy więc, czy zachodzą związki: I

PM|i?C);-PM) i P(P|/IC)s=P(P) i P(C|AB)asP(C)'!

ilość uczniów, którzy zwiedzili dział A i B i C ilość uczniów, którzy zwiedzili dział B i C

Ilość uczniów, którzy zwiedzili działy B i C stanowią trzy części grupy pierwszej -i- jedna I część grupy drugiej-4 części; ilość uczniów, którzy zwiedzili działy A i B i C stanowią I trzy części grupy pierwszej»3 części. Stąd

P(A\BC)-i*P(A),

a zatem zdarzenia nie są niezależne zespołowo.

Przykład 4,6.5. Wycięto z papieru kwadraty i każdy kwadrat podzielono liniami I na cztery części, Mając do dyspozycji cztery kolory; B — biały, C — czerwony, N -niebieski, 7. - zielony, pomalowano każdy kwadrat dowolnym kolorem tak, że kolor I

w danym kwadracie mógł się powtarzać na- I wet cztery razy, np. B, B, B, B; N, B, X, X (rys. 4.6.1), Wycięto tyle kwadratów, ile potrzeba | było, aby otrzymuć wszystkie możliwe składy kolorów i wrzucono je do urny.

1,    Ile kwadratów należało wyciąć?

2,    Czy są niezależne zdarzenia /i, C, N. Z, polegające na tym, że losowo wybrany kwadrat ma odpowiednio kolor biały, czerwony, niebieski, zielony?

I. Iyle należało wyciąć kwadratów, ile jest kombinacji z powtórzę-

p(A\nc)

;>j	Z
B	Z

{tyś. 4,6.1

K oz wiązani*: niami /. 4 elementów po 4

2. Obliczmy najpierw ilość kwadratów, nu których jest kolor biały. Jedna część kwa* drutu musi być pomalowana na kolor biały, pozostałe trzy części na dowolny kolor (spo-

śród danych). Wobec tego sprzyjających sposobów jest tyle, ile jest kombinacji z powtórzeniami z 4 barw po 3, tj. ć|—C|~20. A zatem

p(B)=²£=±.

Wszystkich kwadratów, które mają kolor C jest tyle, ile jest tych, które mają kolor B, tzn. 20.

Odpowiedzmy następnie na pytanie: ile jest wśród kwadratów pomalowanych kolorem C takich, które pomalowano kolorem £? Jest ono równoważne pytaniu: ile jest takich kwadratów, które mają kolor B i C? Jest ich tyle, ile jest kombinacji z powtórzeniami z 4 elementów po dwa, tzn. C\—C\ —10. Wobec tego

P(P|C)=ł,

a zatem

P(B\C)*P(B).

Analogicznie można wykazać, że

P(B\N)=P(B), P(B\Z)źP(B), P(N|B)=P(JV),    P(N|Z)#P(N),

P(N\C)t£P(N),    P(C|£) = P(C),    P(C|Z)#P(C),    P(C|N)#P(Ć),

P(Z|P) = P(Z) I P(Z|C)#P(Z), P (Z | N) # P (Z).

Wniosek. Zdarzenia nie są parami niezależne, więc nie są również niezależne zespołowo.

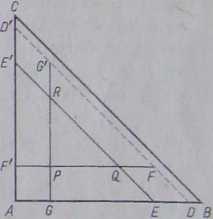
Rys. 4.6.2

czy są niezależne zespołowo?

Przykład 4.6.6. Rozpatrujemy równoramienny trójkąt prostokątny ABC (rys. 4.6.2). Niech AB=AC=16. Obierzmy punkty D i Z)' odpowiednio na boku AB i AC w odległości od /I równej 15. Łączymy Z) z D'. Dalej analogicznie y4£=y4£'=12, AG=AF'=3. Łączymy £ z £' oraz prowadzimy proste (7(7 i ££' równoległe odpowiednio do AB i /te. Załóżmy dodatkowo, iż prawdopodobieństwo trafienia punktu w pewien obszar danego trójkąta jest zależne jedynie od wielkości tego obszaru i proporcjonalne do niego. To, że punkt materialny trafi w trójkąt ABC, uważamy za pewne. Niech E_u E₂, £3 będą zdarzeniami polegającymi na trafieniu punktu odpowiednio w trójkąt AE'E, FF'D', GG'D. Zbadać, czy zdarzenia E_u £₂, £3 są niezależne parami oraz Rozwiązanie.

S&AEB' __	9	HEPiiS
—-~"	Tó»
S&ABC		& & ABC
S&GG'D_	9 16 »
S&ABC		& &FF'D^f