DSCF6641

238

Obserwacja pierścieni Newtona w ciekłych kryształach posłużyła do badania ich dwójłomności. Widziane są wówczas podwójne pierścienie spolaryzowane we wzajemnie prostopadłych płaszczyznach.

3. Pomiary i opracowanie

Światło lampy sodowej, po odbiciu od płytki szklanej ustawionej pod kątem do poziomu, pada na badany układ (rys. 90).

lampa sodowa

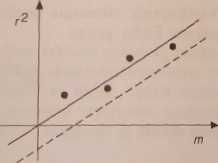
Rys. 91. Liniowa zależność pomiędzy kwadratem promienia prążka i jego „numerem”

Pierścienie obserwowane są przez mikroskop zaopatrzony w śrubę mikro-metryczną, pozwalającą odczytywać przesunięcia tubusa w płaszczyźnie poziomej. Pomiary polegają na określeniu promieni kilkunastu ciemnych prążków. Równanie 2 można sprowadzić do postaci liniowej y = am przez podstawienie y = r¹, a = RA.

Metodą najmniejszych kwadratów lub graficznie znajdujemy współczynnik a nachylenia prostej oraz, odczytując długość fali światła sodowego z tablic, promień krzywizny soczewki R = a/A. Ponieważ wartość | znana jest bardzo dokładnie, można przyjąć, że AR/R = Aaja. Może się zdarzyć, że punkty doświadczalne będą się układały na prostej przesuniętej względem początku układu współrzędnych (linia przerywana na rys. 91). Przyczyną może być obecność drobin kurzu uniemożliwiających „punktowy” kontakt soczewki z płytką. W przypadku zastosowania graficznej metody wyznaczania współczynnika nachylenia prostej nie ma to żadnego wpływu na wynik.

jjjli natomiat obliczenia wykonywane są metodą najmniejszych kwadratów, wówczas należy poszukiwać dwuparametrowej prostej opisującej wyniki pomiarów; y = am + b.

pytania

1.    Czy w proponowanej metodzie pomiaru niezbędna jest znajomość „bezwzględnego numeru” pierścienia, tzn. odliczanie od początku układu?

2.    Jaki byłby stosunek promieni pierścieni o danym numerze obserwowanych w świetle z dwu krańców zakresu widzialnego? (ok. 0,38 jzm i 0,76 /an).

3.    Pierścienie Newtona można obserwować nie tylko w świetle odbitym, lecz także w świetle przechodzącym. W którym wypadku większa będzie jasność pierścienia, a w którym obraz będzie bardziej kontrastowy?

0-3. Sprawdzanie wzorów Fresnela [40-42] ¹

1

Wstęp

Rozpatrzmy przechodzenie światła przez granicę dwu przezroczystych ośrodków o współczynnikach załamania n, i r₂ (rys. 92).

Przepływ energii przez jednostkę powierzchni w jednostkowym czasie wynosi:

S = B₀cnE²    (I)

gdzie E oznacza natężenie pola elektrycznego, n i c odpowiednio współczynnik załamania i prędkość światła, a e₀ - przenikalność dielektryczną próżni.

Jeśli wiązka pierwotna pada pod kątem Oj na granicę ośrodków o współczynnikach załamania i n₂, wówczas energia docierająca w jednostce czasu do jednostki powierzchni rozdzielającej ośrodki wyniesie:

J® = S® cos a, = e₀cn₁1^4|² cos a_:    (2)

gdzie A oznacza amplitudę fali padającej.