DSCN1119

3.20. Wskazówka. Należy wykazać, że

a + c

jest średnią aryt

metyczną liczb b + c a + b’

3.21. Z własności ciągu arytmetycznego

_t log_kx + log_rx logm* =-ó-

Stąd na podstawie wzoru log_ab —

log_ba

Po pomnożeniu obu stron równości przez log^/c log^n otrzymujemy

2 log_mx log_xfc log_xn = log_x(fcn).

Zatem

2 log^fc log_xn = log_x(fcn).

Po podzieleniu obu stron przez log_xn mamy

Na podstawie wzoru log. b =    -

log.a

mamy

2 logJc = log_H(kn).

Stąd

kn = n^2,0«-* czyli n² = (knf** = (knf°^gkm.

3.22. Wskazówka. Przyjmując x² = t,(t^ 0) otrzymujemy równanie:

(2) t² - (3k + 2) z + fc² = 0.

Aby rozwiązania równania, danego w treści zadania, tworzyły ciąg arytmetyczny musi ich być co najmniej trzy.

Dane równanie ma trzy rozwiązania tylko wówczas, gdy równanie (2) ma dwa rozwiązania postaci fj = 0, f₂ = ^a-> gdzie a > 0. Stąd otrzymujemy warunek: k = 0. Wtedy rozwiązaniami danego równania są liczby -yjl, 0, y/l i rozwiązania te tworzą ciąg arytmetyczny.

Dane równanie ma cztery rozwiązania tylko wówczas, gdy równanie 2) ma dwa różne rozwiązania będące liczbami dodatnimi . Oznaczmy te rozwiązania przez f,, t₂ i załóżmy, że f, > t₂-Wtedy kolejnymi wyrazami ciągu arytmetycznego będą liczby —y/ti, —y/h’ y/h> \fh- Teraz wykorzystując wzory Viete’a i własności ciągu arytmetycznego wyznaczymy k, otrzymując

ki ~ 6, k₂ — — Yę'

Odp. fce j—0, 6j.

3.23. Z warunków zadania wynika równanie

(1) 5-5' + A + ₅²* + ^ = p,

czyli 5(5*+ p) + 5^J* + ^ = _P.

Oznaczając przez r sumę 5* + — otrzymujemy

t² — 2,

zatem równanie (1) przyjmuje postać (2) t² + 5f-p —2 = 0.

Z kolei mamy:

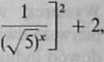
⁵'⁺?-^[('^/S'^{], +} r<yfe

a stąd wynika, że

(v#

dla xe.R 5^X +    e <2; 00).

5

W takim razie warunkiem koniecznym spełnienia warunków zadania jest to, by równanie (2) miało co najmniej jedno rozwiązanie nie mniejsze niż 2.

A tak będzie dla p e <2; 00).

3.24. Wskazówka. Oznaczając pierwiastki wielomianu przez x — r, x, x + r mamy:

|x-r + x + x + r = 3x 1 (*-r) *(* + /*) = 315,

95