DSCN1129 (2)

Rozważmy teraz drugą z danych nierówności.

Po przekształceniu jej otrzymujemy nierówność (x - 2/c)^a - k > 0.

Stąd wynika, że zbiorem rozwiązań drugiej nierówności jest zbiór

jR dla k <0,

l(—oo; 2k - yjk ) u <2/t +    oo) dla k > 0.

Z powyższych rozważań wynika, że warunek zadania spełniają na pewno te parametry /c, których wartości należą do zbioru (— oo; 0> u {1}. Pozostają jeszcze do zbadania dwa przypadki: 1)|e(0» 1); 2) ke(\; oo).

W przypadku 1) warunkiem wystarczającym na to by suma zbiorów rozwiązań obu nierówności równała się R jest spełnienie alternatywy

5* - 2 > 2* + s/k lub k + 2 « 2k - y/k.

Nietrudno jest stwierdzić, że nie istnieje ke(0; 1) spełniające tę alternatywę.

W przypadku 2) wystarczy spełnienie alternatywy k + 2 > 2k + jk. lub 5łc - 2 « 2k - ^/k.

Okazuje się, że i w tym przypadku nie istnieje ke( 1; oo) spełniające tę alternatywę.

W takim razie sumą zbiorów rozwiązań danych nierówności jest R wtedy i tylko wtedy, gdy fte(— oo; 0)0 {1}.

4.41. Wskazówka. Z pierwszego równania wyznaczamy x: x = by — az².

Po podstawieniu otrzymanego wyrażenia w miejsce x, do drugiego równania, mamy 2bz¹ + 8z + 8 ^y “ (26 - 3)(fr + 2)'

Widać stąd, że dla każdego be jR\<-, — 2> układ ma rozwiązanie. Wystarczy bowiem obrać dowolnie z, a następnie obliczyć x oraz y.

_t 3    . _w    2

Jeśli b =b -, to układ ma rozwiązanie tylko wówczas, gdy a < - •

Zatem układ ma rozwiązanie dla każdego b e R wówczas, gdy

4.42. ae <    3) vj {7 - 4^3, 7 + 4^/3}.

4.43. Wskazówka. Zbiór rozwiązań układu ma prostą interpretację geometryczną. Jest to bowiem zbiór punktów wspólnych brzegu kwadratu o wierzchołkach (1, 0), (0, 1), (— 1, 0) (0, — 1) i okręgu o(0, y/a).

Dany układ:

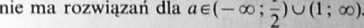
4.44.    Jeśli dany układ ma rozwiązanie (x,y), to {px + qy)² = l².

Stąd

1)    p²x² + 2pqxy + q²y² = 1.

Po odjęciu stronami równania 1) i pierwszego równania danego układu otrzymujemy

2)    (p² - a)x² + 2pqxy + (q² - b)y² = 0 Para {x,y) spełnia równanie 2), więc A ^ 0.

Ale A = 4p²q²y² — 4{p² — a) (q² — b)y² = 4y²(bp² + aq² — ab). Zatem z warunku A ^ 0 wynika nierówność bp² + aq² — ab ^ 0. Stąd

ab <    + bp².

4.45.    Układ ma dokładnie jedno rozwiązanie dla k # — 2 i k # 1 i dowolnego a, b, c.

Układ ma nieskończenie wiele rozwiązań dla k = —2ia + b + c = 0 lub dla k = 1 i a — b — c.

Układ nie ma rozwiązania dla (k = —2 i a + b + c ^ 0) lub dla (k = 1 i a # b lub a # c lub 6 # c).

115