CCF20081203028

Stąd po przekształceniach

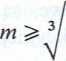
2M_obi -ą-cosP X-z- kgj

(11.74)

Z dotychczasowych rozważań wynika, że zarys zębów w kole skośnym o liczbie zębów z odpowiada zarysowi zębów prostych w kole o liczbie zębów z_z. Dlatego do wzoru 11.74 podstawia się współczynnik kształtu zębów q, obliczony dla z_z.

Obliczanie nacisków powierzchniowych w kołach o uzębieniu skośnym wykonuje się wg wzoru 11.55

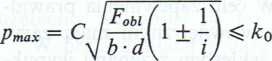
wprowadzając odpowiednio wartości F_obl oraz b wg objaśnień podanych przy omawianiu rozkładu sił.

Zastosowanie przekładni walcowych o zębach skośnych i daszkowych. Przekładnie walcowe skośne i daszkowe znajdują obecnie coraz szersze zastosowanie, głównie ze względu na swoje zalety w porównaniu z przekładniami walcowymi o zębach prostych.

Do podstawowych ich zalet zalicza się:

•    bardziej równomierny przypór, powodujący większą płynność zazębienia oraz większą cichobieżność,

•    zdolność do przenoszenia większych obciążeń, wynikającą z możliwości uzyskania większej liczby przyporu oraz z korzystniejszego zarysu zębów,

•    możliwość stosowania dowolnego kąta pochylenia linii zębów, co umożliwia zwiększenie rozstawienia osi bez zmiany liczby zębów.

Podstawową wadą przekładni z kołami o uzębieniu skośnym jednokierunkowym jest występowanie siły osiowej F_w (rys. 11.20). Siła ta powoduje obciążenie łożysk dodatkową siłą wzdłużną. W przekładniach z kołami jednoskośnymi stosuje się kąt fi ^ 20°. Przy wartości kąta fi < 9° można stosować łożyska toczne poprzeczne, które mogą przenosić pewne obciążenie wzdłużne, gdy zaś kąt fi > 9°, należy stosować łożyska skośne lub jednocześnie łożyska poprzeczne oraz wzdłużne.

W celu uniknięcia wpływu sił osiowych na pracę łożysk stosuje się koła daszkowe. W obydwu uzębieniach takiego koła (lewym i prawym) przyjmuje się tę samą wartość kąta fi — ale o przeciwnym kierunku. W tym przypadku siły poosiowe znoszą się, zbędne jest stosowanie łożysk wzdłużnych oraz można przyjmować większe wartości kąta fi (wyjątkowo nawet do 45°), co w myśl dotychczasowych rozważań znacznie zwiększa zalety tych przekładni.