DSCN1149

Skąd po przekształceniach otrzymujemy równanie 2sin²^ -f y/Ssin^ —1=0,

którego rozwiązaniami są:

. a -72 + 710    . a -s/I-^lÓ

sin - = —-—-—-—, sin---i---^v

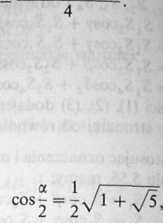
2    4    2

Zatem

cos a = 1 — 2ł ——- —— 1 ; skąd

v/5-l cosa =    -—.

A dalej

1    ^co^ ⁼ 2jk’

skąd po przekształceniach otrzymujemy:

4

5.59. NiechS = P^abc^i ~ ^b.abd*^2 ⁼ ^s.bcd^3 ⁼ ^^/4i>c(^ry^s*5.59).

0

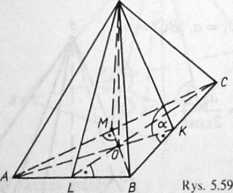
Z warunków zadania wynika, że AOKD s AOLD 2 AOMD.

Stąd

|OK| = |OL| = |OM|,

a więc O jest środkiem okręgu wpisanego w A ABC.

Oznaczmy długość promienia tego okręgu przez r. Ponadto

\DK\ = \DL\ = \DM\ = h, więc

2S_X = h-\AB\, 2S₂ = h\BC\, 2S₃ = h-\AC\.

Zatem

2ph = 2(S_l 4- S₂ 4- S₃), gdzie 2p = |v4B| 4- |BC| + \AC\. Z drugiej strony p • r = S, wobec tego

r rp    S

cos a = - = — = ---— C

h hp Si 4* S₂ + S₃

gdzie a oznacza miarę kąta dwuściennego.

W takim razie

. ₂    S²

SITTOC = 1 — —---— =

(Si 4- S₂ 4* S₃)

_ (Si + S₂ + S₃ + S)(S_l 4- S₂ + S₃ - S)

Ponieważ

P = więc

(S_x 4- S₂ 4- s₃y

Si + S₂ 4* S₃    2St    **** i 4*11

-—r—^ł. MB| =    , |BC| = HU

2s;

h

2S2 h ¹

,-_Me|,ŁŁŁA. _p__|SC|.£l±4^,

r-\AQ-Wobec tego

S1 4- S₂ — Si

-i

, /(Si + s₂ + S₃)(Si 4- S₂ - S₃)(S, + S₃ - sjfó* +    - s,)

Z.⁴

Jeśli przez H oznaczymy wysokość ostrosłupa, to H² = h²- sin²a.

Ostatecznie otrzymujemy:

K=

ysgj + S₂ 4- S₃ - SH5_t -ł- S₂ 4- S₃ - S) 3(5, +S₂+S₃)

(Si 4- S₂ 4- S₃)(Si 4- S₂ — S₃)*(5j 4- S₃ — S₂)(S₂ 4- S₃ — 5,).

155