490575045
54
M. Mokwa
z której po przekształceniu otrzymuje się:
ksjz = (26nD)6 (17)
Należy w tym miejscu wyróżnić inną formę wzom (15) preferowaną przez Rickerta przy obliczaniu naturalnych koryt rzecznych o przekroju złożonym:
1
&
2 log
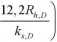
(18)
Odpowiedzi na pytanie, która formula jest bardziej wskazana przy wymiarowaniu „obiektów sztucznych", tj. budowanych przez człowieka przepławek, może dostarczyć weryfikacja wzorów, np. na drodze pomiarów laboratoryjnych. Sumaryczny współczynnik oporów dla roślin (szczotek) XR oraz dna i ścian koryta XD wynika z superpozycji Einsteina/Banksa:
% = XD+XR (19)
W celu obliczenia prędkości średniej, a w dalszej kolejności wydatku przepławki skorzystać można z klasycznego wzoru Darcy-Weisbacha:
(20)
V*=p/WT
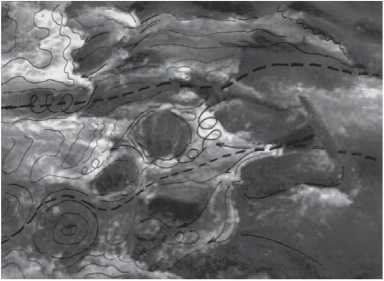
Rys. 8. Model rozkładu strug w przepławce uformowanej z luźno ułożonych głazów Fig. 8. Model of stream distribution in a fishway built from loosely disposed boulders
Acta Sci. Pol.
Wyszukiwarka
Podobne podstrony:
POLITECHNIKA LUBELSKA Po przekształceniu otrzymuje się: Rt= ~R1+~_(Rw+RP+ ^
Zdjecie1096 lub inaczej (Oxsy ~ (a + r sin a)1 + j/i + r • (l ■ cos#)]* Po porównaniu i przekształce
Image0088 BMP Po wykonaniu szeregu przekształceń, otrzymuje się dla mocy czynnej rozpatrywanego odci
5.4. REZONANSOWE UKŁADY KOMUTACJI WEWNĘTRZNEJ 243 Po dokonaniu przekształceń otrzymuje się następują
MG!77 Po jej przekształceniu otrzymuje się wzór, na podstawie którego wyzna, się współczynnik
(4.25) moment (4.26) Po uporządkowaniu otrzymuje się wzór określający długość ramienia a: [ a = kc +
to przy H = const po całkowaniu otrzymuje się, że gdzie: Mx = Cc" = 0,098 -106 = 0,98 • 105 A-m
CLEBSCH 5 Po scałkowaniu otrzymuje się: x3 EIv = C + Ra— +MAx-p — AB X2 A EIv = C
2 (2298) Str. - 2 A po podstawieniu: i, j = 1,2 otrzymuje się: II P = 2n2m0 p,J =< pn = ~(nxm2 +
dTR dQ = P Po przekształceniach otrzymujemy: Wyrażenie jest odwrotnością cenowej elastyczności
PB250320 d(lnk, - lnk2)_ Ey> -E(a2) dT ~ RT2 Po przekształceniu otrzymamy dlnk, Ęg> _dlnk2 E(A
Rozdział 1axb = (1.4) Po przekształceniach otrzymujemy: (1.5)axb = [a b — a b ,-a b +a b ,a b — a bR
§ 1. Teoria elementarna 579 z której daną całkę otrzymuje się dla y — 1. Założenia twierdzenia 3 będ
CCI20091105�002 132 8. Hydrauliczne obliczanie przewodów pod ciśnienia Po porównaniu (8.7) z (8.8) o
więcej podobnych podstron