CLEBSCH 5

Po scałkowaniu otrzymuje się:

x³

EIv' = C + R_a— +M_Ax-p —

AB

X²    _A

EIv = Cx + D + R_a— + M_A —    p —

Uwzględniając warunki równowagi:

a)    x = 0, (p_A = 0 (kąt obrotu na podporze A równa się zeru),

b)    x = 0, v_A = 0 (ugięcie na podporze A równa się zeru), otrzymuje się C = 0, D = 0.

p/²

Po podstawieniu R_A = pl, M_A=--—, a także C = 0, D = 0, otrzymuje się:

, x² pl² x³

EIv-,pl_T-—_x-p—

X³    pl² x²    x⁴

^y 6    2 2    24

Przemieszczenia końca belki wyniosą: - kąt obrotu przekroju B (x = l)

<Pb = Vb =

_L(p?_ EI\ 2

pŁ

2

ilL

6 El’

- ugięcie przekroju B (x = l)

_v __LP^l*\₌    P^l4

^B El \ 6    4    24 y 8£/ ■

Podstawiając dane:

I

bh³

12

12-18³ 12

= 5832 cm⁴,

l = 200 cm, p = 0,025 kN/cm, E = 1000 kN/cm²,

uzyskuje się:

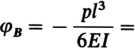
0,025 -200³ 6 1000-5832

v_B

= —0,0057 rad,

pl⁴ 8E7

0,025 • 200⁴ 8-1000-5832

— 0,86 cm.

Warunek (8-10) jest spełniony, gdyż

v_B = 0,86 cm < a_dop = 1/200 = 200/200 = 1,0 cm.