P1070057

134 Czfdć 11. Rozwiązania i odpowiedzi

a zatem

dp = p(<o² rdr—gdz).

Po scalkowaniu otrzymanego równania różniczkowego:

p

p = -w²r²—pgz + C,

gdzie dla r = 0 i z = z₀, ciśnienie p - p,, czyli stała całkowania

C = p₀+pgz.-

W związku z tym, zależnością opisującą rozkład ciśnienia jest następujące równanie:

p

p = Po-py(z-^zo)+-°>^2rZ-

2.2.3. a. Równanie różniczkowe powierzchni ekwipotencjalnej, w układzie współrzędnych cylindrycznych, ma następującą postać:

dp

= (q_rdr+q,rdS+9_rdz) = 0,

gdzie składowe wypadkowej jednostkowych sił masowych wynoszą: ą, = (0²r, q_s- 0, ą, = -g\ stąd

(o²rdr—gdz = 0.

Po scałkowaniu mamy

oj²r²

——gz = C.

Z warunku

z = z₀ dla r = 0,

wyznaczamy stałą całkowania

C - -gz„

zatem równanie powierzchni ekwipotencjalnej jest paraboloidą obrotową opisaną równaniem:

-g{z-z_e) = 0.

b. W układzie współrzędnych prostokątnych r² = x²+y².

wobec tego równanie powierzchni swobodnej przybierze postać

(O³

Y(x²+r)-g(2-zJ = 0 lub

x^a+y³--r(z-rj«0.

ar

2JL4. W równaniu różniczkowym powierzchni ekwipotencjalnej

Xdx+ Ydy+Zdz ~ 0,    (1)

rzuty jednostkowej siły masowej P, w przyjętym układzie współrzędnych (rys. 11-2.6). wynoszą:

X = a, Y= 0, Z = —g.    (2)

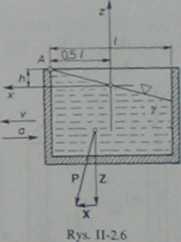
Po podstawieniu wyrażeń (2) do zależności (1) i scal kowani u otrzymamy równanie powierzchni swobodnej cieczy

a

z*=-x.    (3)

9

Korzystając z równania (3) oraz wiedząc, że powierzchnia swobodna cieczy powinna przechodzić przez krawędź zbiornika, tj. punkt A (1/2, h\ wyznaczamy opóźnienie maksymalne, a zatem dla z = h oraz x = //Z

h

a_..ł 2g '

stąd

2gh

~T'

(4)

(5)