P1070063

146 Crdi II. Rozwiązania I odpowiedzi

n(D* — d*) n,^D2+dl ¹⁶⁰'

64--U

4

e) Całkowite pole powierzchni figury

I = S | 4R¹ = 11    + 4^ * 5,57R²,

a współrzędna środka ciężkości

<4|ZSi+^2^ZSj

^Zs“ A

czyli

R « 1,6R.

R² U+4

3tc + 44 3n + 24

Moment bezwładności figury względem osi x, wynosi:

\nR* mm%

^Ix' “2 4 ⁺    3

= R⁴(| + y)*5,73K⁴,

natomiast moment bezwładności względem osi centralnej x„, obliczamy z twierdzenia Steinera, a zatem

I_Xo = I_Xi-A(z₅-R)²,

czyli

gg = 5,73/?“—5,57R²(1,6R - R)² « 3,737?“. Silą naporu obliczona ze wzoru (1) wynosi

P = y5,57/?²*l,6/? = 8,91y/?³, a położenie środka naporu (według zależności (4)):

3 73R*

4 i ! nR² , mi

x_s = _2s = --,    1—,    ,

nR²4R y/?³

^V 4 3n “ 3 '

2. Sl»tyk« płynów_147

Współrzędną z_c położenia środka naporu wyznaczymy ze wzoru (2), wobec tego

nR* 3n _n ^{Zc =} _tnR² 4 R~Tó^R‘

^,6T3«

Współrzędną x_c obliczamy z następującej zależności

I_xx jest momentem dewiacyjnym, który dla czwartej części koła wynosi:

r3    £ 4

I_xt = J Jr^Jsinę>COSę>drdę> = —,

n n

zatem

R⁴ 3

^{XC =} 8--— ⁸ V 3% 4

2.3.6. Środek naporu C (rys. II-2.13) znajduje się na głębokości

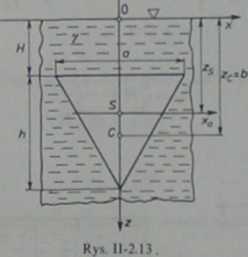
Według twierdzenia Stcinera

/, = /,.+/łz|;

stąd

= b

l*. + *^zs

Az_s

^zs +

^^zs'