P1070056

132_Część II. Rozwiązania I odpowiedzi

Zgodnie z zależnością wyprowadzoną w poprzednim przykładzie

132_Część II. Rozwiązania I odpowiedzi

a zatem

gil

Pu = />.e“KT,

1-

P.^e

■ = 0,03.

(2)

(3)

lU

_e-*T = 0,97;

Po przekształceniu wzoru (3) otrzymamy: stąd

RT

H ---ln 0,97.

9

(—0,03045) = 261 m.

H = -

Po podstawieniu wartości liczbowych otrzymamy: -287-293

9,81

2.1.17. Dla izentropowego uwarstwienia powietrza obowiązuje następująca zależność:

p

—r = const,

P

gdzie k jest wykładnikiem izentropy. W związku z tym P₀ \P.J *

czyli

P = f) .    (1)

\PoJ

Dla takich samych warunków brzegowych, jak w przykładzie 2.1.15, otrzymamy:

*n "

0tf+Jy = °.    (2)

pi,

Z podstawienia wzoru (1) do równania (2) otrzymamy:

skąd po scałkowaniu i przekształceniu, wyznaczamy ciśnienie atmosferyczne na wysokości H, a zatem

(t ^k~^l Pq9^h\£t

i——J

2.2. Równowaga względna cieczy — powierzchnie ekwipotencjalne

2.2.1. a. Przyspieszenie wagonika jest równe gsina (rys. II-2.5), zatem jego prędkość

v = gt sin a.

b. W ruchomym (względnym) układzie odniesienia, składowe jednostkowej siły masowej są równe g oraz 9 sin a, przy czym zwrot tej ostatniej jest przeciwny do kierunku ruchu (rys. II-2.5). Wynikiem dodawania wektorów składowych jest wypadkowa jednostkowych sił masowych o module g cos a.

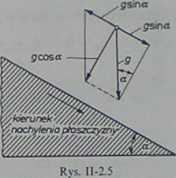
c. Na powierzchni wody p = p_a = const i wypadkowa jednostkowych sił masowych jest prostopadła do płaszczyzny równi, wobec tego kąt ę = 0.

2.2.2. Poszczególne człony podstawowego równania hydrostatyki, zapisanego w układzie współrzędnych cylindrycznych

— = q.dr+q₉rd9+q_xdz,

P

są odpowiednio równe: