243

5.4. REZONANSOWE UKŁADY KOMUTACJI WEWNĘTRZNEJ 243

Po dokonaniu przekształceń otrzymuje się następujące wzory, umożliwiające obliczenie pojemności C_K i indukcyjności L_K obwodu komutacyjnego przy największym prądzie obciążenia I_m i najmniejszym dopuszczalnym czasie komutacji

5.4. REZONANSOWE UKŁADY KOMUTACJI WEWNĘTRZNEJ 243

Ck —

min ^e

,*/4Q

2 [/_co arccos

Lk —

2x1 _m arccos

T

— e~^n/4eJ

(5.104)

(5.105)

W przypadku dużej dobroci obwodu komutacyjnego (Q $= 3) wartości C_K i L_k mogą być obliczone następująco:

C,

1

X

2K ₂ arccos —

(5.106)

(5.107)

1

^r --w _

-‘K ~    j

2K _l x arccos —

gdzie

K, =

co

UcoT_Kmin

Wykres zależności (5.106) i (5.107) przedstawiono na rys. 5.22.

I T

m Kmin

(5.108)

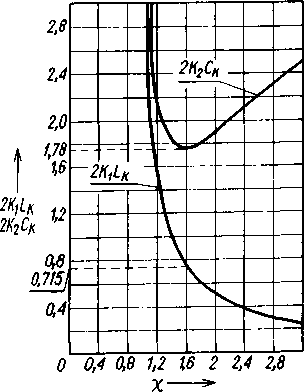
Rys. 5.22. Wykres zależności L_K = f(x) i C_K = f ( -/) układu komutacji z dławikiem w obwodzie kondensatora