img030

CAŁKOWANIE FUNKCJI WYMIERNYCH

Po tym przekształceniu otrzymujemy:

CAŁKOWANIE FUNKCJI WYMIERNYCH

dx

-J

dx

<2x

(cu²+i>x+c)

Teraz stosujemy całkowanie przez podstawienie (twierdzenie 2.5):

, , 2a b ⁺ V=A^X+V=A

. . 2a b

^+l V=a^X+V=K

		■J-A \
=f-T		^2a dt
Ia J	J
		y

la b    V^A    t

t = -₇=x+-—=<f__x(t\x =-1--=((</)

V-A    V-A    2a    2a

_;V=Ą

2a

<p'(r) =

(1 + /²)

i gdy n > 1, korzystamy ze wzoru rekurencyjnego (3.7), gdy zaś n = 1, stosujemy wzór 9 z tablicy 1.

4. Podstawiamy obliczone całki / oraz K_n do wzoru (*) i otrzymujemy szukaną całkę z ułamka prostego II. rodzaju:

(3.8)

J

Ax+B

+bx+c^lj

dx =

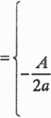
A, | 2    . I (_D zlM 2    2ax+b

_łto+c|^S-_J-^arctg^—,    gdy„-l,

^1 iffl ^2 rv*	( \ f *
(n-l)(ar^2+&r+c) l	l^JM‘J

(A, B, a, b, c, e R, n e N, A = b²- 4ac < 0).

PRZYKŁADY

xdx

^J 2* -r + l ^J 2x -x + l    4^J 2x -x+l    l + 2(x--\

A = -7 < 0

= —ln(2jt^I-^ + l)+2 — f-—-y = I|n(2i¹-jc+l)+— [ —-

4    4 ₇J _{1 +}    4    7J₁₊(

dx

u

30