DSCF6631

218

Po kilku przekształceniach otrzymamy wynik:

i XŹR_L-iX_c(Rl+Xl-X_LX_c) ggf    Ri+(X_L-X_c)²

Po wykonaniu podobnych, chociaż znacznie żmudniejszych działań, można znaleźć zawadę całego obwodu, a następnie stosunek napięcia wyjściowego do wejściowego (por. rys. 79):

|£ | A(A + D) + B²-iBD Ig    (A + D)² + B²

gdzie: A = XlR_L,

B = RlX_c + X_LX_c(X_L-X_c), D = R_SR²L + R_S(X_L-X_C)².

Moduł tego zespolonego stosunku napięć ma wartość:

{[A(A + D)+B²]² + (BD)²}¹'²

|A + D)² + B²    p

Dla częstości rezonansowej, co = co₀, zawada staje się rzeczywista, tzn. znika część urojona wyrażenia 2:

R²L + Xl-X_LX_C = 0    (5a)

Po wykorzystaniu wzoru 1 wynika stąd wyrażenie na częstość rezonansową:

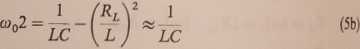
Ostatnie przybliżenie otrzymaliśmy przyjmując L ,

ckT¹

(założenie a). Wyrażenie 4 przyjmuje wówczas postać: v_a = A(A + H)²+K gdzie: H = R_sR²L + ^^jQ|

Hii!

a>0 (O '

(indeks przy v odnosi się do przyjętego założenia). Przy częstości rezonansowej

a = K = 0;    H = R_sRl

a wartość stosunku napięć jest maksymalna:

_v -_A__ilpKr¹

^Va:m~ A+H~Iww;

(7)

Jeśli teraz drugi składnik H jest znacznie większy od pierwszego:

R*Lęi²

»R_SR² czyli L/CRl»a~²

(założenie b) oraz dodatkowo czynnik A jest mały w porównaniu z H: A/H « 1, czyli RlI[((oI(o₀)² — l]^z « R_s (założenie c), wówczas równanie 4 sprowadzi się do postaci:

li

(8)

Zauważmy, że w przypadku, gdy pierwszy składnik licznika jest pomijalnie mały w porównaniu z drugim (założenie d), wówczas otrzymamy wyrażenie odpowiadające przypadkowi cewki idealnej:

-Hm

-i

które przyjmuje dla to = oi₀ wartość maksymalną v_aM;me, = 1.

(9)