76 (195)

160    Przekształcenie Laplace a

Po prostych przekształceniach otrzymamy

s (s + 2)²+3² (s + 2)² + 3²

F(s) = - — 2 ■ ,⁵+,².    +3,

Ponieważ

(_{s + 2})2 + ₃² “ ^C ^ ²'^cos3<} •

więc

•(s + 2)² + 3² f(t) = (2 — 2e^-2* cos 3t -p 3e^-2t sin 3<) 1(<).

= C {e ²¹ sin 3i} ,

Zadania

) Zadanie 12.1

Korzystając z własności przekształcenia Laplace’a wyznaczyć transformaty podanych funkcji:

c) /(i) = V coswt;

=    o)”;    b) /(<) = < sin ud;

cos uit — 1 < ^;

f) /(O =

^d) /(O = t(_si_n( ₊ (cos();    e*) /(() -

«♦)/(<) = /^*.

0

> Zadanie 12.2

Naszkicować podane oryginały i znaleźć ich transformaty Laplace’a: dla 2n ^ t < In + 1, dla 2n -p 1 ^ i < 2n + 2,

— 2n    dla 2n^t<2n+l,

-t -+- 2n -P 2 dla 2n -P 1 ^ t < 2n -P 2, c) f(t) = max{sinwt,0}.

a)    m

b)    m

-{‘i

gdzie n = 0,1,2,... ;

gdzie n = 0,1,2,... ;

Zadanie 12.3

Wykorzystując całkę Laptace’a obliczyć podane całki niewłaściwe:

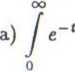
cos irt dt;

7 _i

b) / e ² (t⁴ — 2i² -P 4) dt-, 0

00

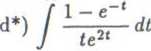
o

Zadanie 12.4

Metodą rozkładu na ułamki proste znaleźć oryginał, gdy:

a) F(s) =

s³ — 3s¹ — 7s — 8 (s+ l)¹(s¹ +4)

; b) F(s) =

\ rt \ ds¹ "b 20s + 26    _JX n/ s

^c) ^ ^{5 =} s(s¹ + fis + 13) ’    ^d)F(s) =

Odpowiedzi i wskazówki

4s³ + 9s¹ + 8s + 2 s(s + 2)(s¹ + 1) ¹ 3s³ — 8s¹ + 21s — 8 (s - 2)¹(s¹ + 2s + 5)'

^{2    ,}-¹'    ₃²    jr    _s

s"+> ’    (s¹ + w¹)¹’    (s¹+u,¹)³ ’ ^d) (s¹ + 1)2 ^{; e#)} 2 “ ^arCtgJ^;

-i o i \ n a n!    2suf ^ 2s(s 3u> )

^{12 1 a}) ^{a c} 7^77 • b) ;._a , .w ^c) -7.2 ■ .;

f*) ln .. _ _; g*) -    — arctg—^ .

VV + w¹    J \ 2    ^Bw/

...»»> (i-«-y _n i (i --y , «

^12,2 )    -2 '    — a» ^,c) ₅2_+w2

s (] — e^-2s) ' s² 1 — e'

1 — e

.    1    .    . 2\/3 — 1    . 3

^{12.3 a)} TT^^{; b) 744; c)} ~io~^] d } ln 2‘

12.4    a) — te~^l + cos 2< — 2sin 2<; b) 1-f e^-2< +2 cos t-f 3 sin i; c) 2 + e~³¹ sin 2t + 2e~^3< cos 2<; d) e²¹ + 2te²¹ + 2e~‘ cos 2t - 2e^-' sin li.

Trzynasty tydzień

Przykłady

• Przykład 13.1

.niJuuuTilnuajiKiłti.it • >luHtBł*RWi.lul

Metodą residuów wyznaczyć oryginały, których transformatami są podane funkcje:

a) F(s) =    ■ ~¹ —x; b) F(s) = -—--_s.

’ ^w (s² + l)¹    (s- l)(s²+2s + 5)¹

Rozwiązanie

W podanych rozwiązaniach będziemy korzystać ze wzoru

n

f(t) = C~' {F(s)} = ^ ^res», [/’(«)«“] dla i > 0,

gdzie si,S2,...,Sn są biegunami funkcji F(s).

—2

a) Funkcja F(s) = -=- ^ma bieguny dwukrotne » oraz —i. Obliczmy residuum funkcji

(s² + 1)

F(s)e^,‘ w pierwszym z tych punktów. Mamy

res, [/-(sje⁵'] = lim —

= lim —

a —i U3

(s - «)¹

-2

(s - »)¹(s + j)¹

-¹

(s + t)

= lim

a—*i

(³ + *)

(s + .)¹

*    , 1 . ic

= -e + -te .

1

2