elas 7

stąd

W₄ (/) -Al 2 sin 2a[sin(<y / + A) - sin <y/],

a po przekształceniu tożsamości otrzymuje się

W_Ą{t) = A -sin(r^/ + A/2) sin 2a-sin(A/2)    (6)

Chwilowa wartość wychylenia drgań sinusoidalnych z częstością odpowiadającą kwantom, np. światła sodowego³ nie jest oczywiście możliwa do zarejestrowania. Wzrok obserwatora lub klisza fotograficzna zareaguje na wartość skuteczną strumienia świetlnego <&_A proporcjonalnego do kwadratu wychylenia

O . = k#-Wj =[/t_<I,-^²-sin²(«/ + A/2)]-sin²2a'Sin²(A/2)    (7)

W wyrażeniu (7) człon wzięty w nawias kwadratowy jest dla wzroku ludzkiego pewną wielkością stałą, zależną wyłącznie od strumienia świetlnego emitowanego przez oświetlacz polaryskopu oraz od przejrzystości układu optycznego polaryzator - model - analizator. Oznaczając ten człon przez ć, otrzymuje się wygodną do dyskusji formę na strumień świetlny spolaryzowany za analizatorem

O, = <5 • sin “ 2 a • sin

* 1

9

(A/2)    (8)

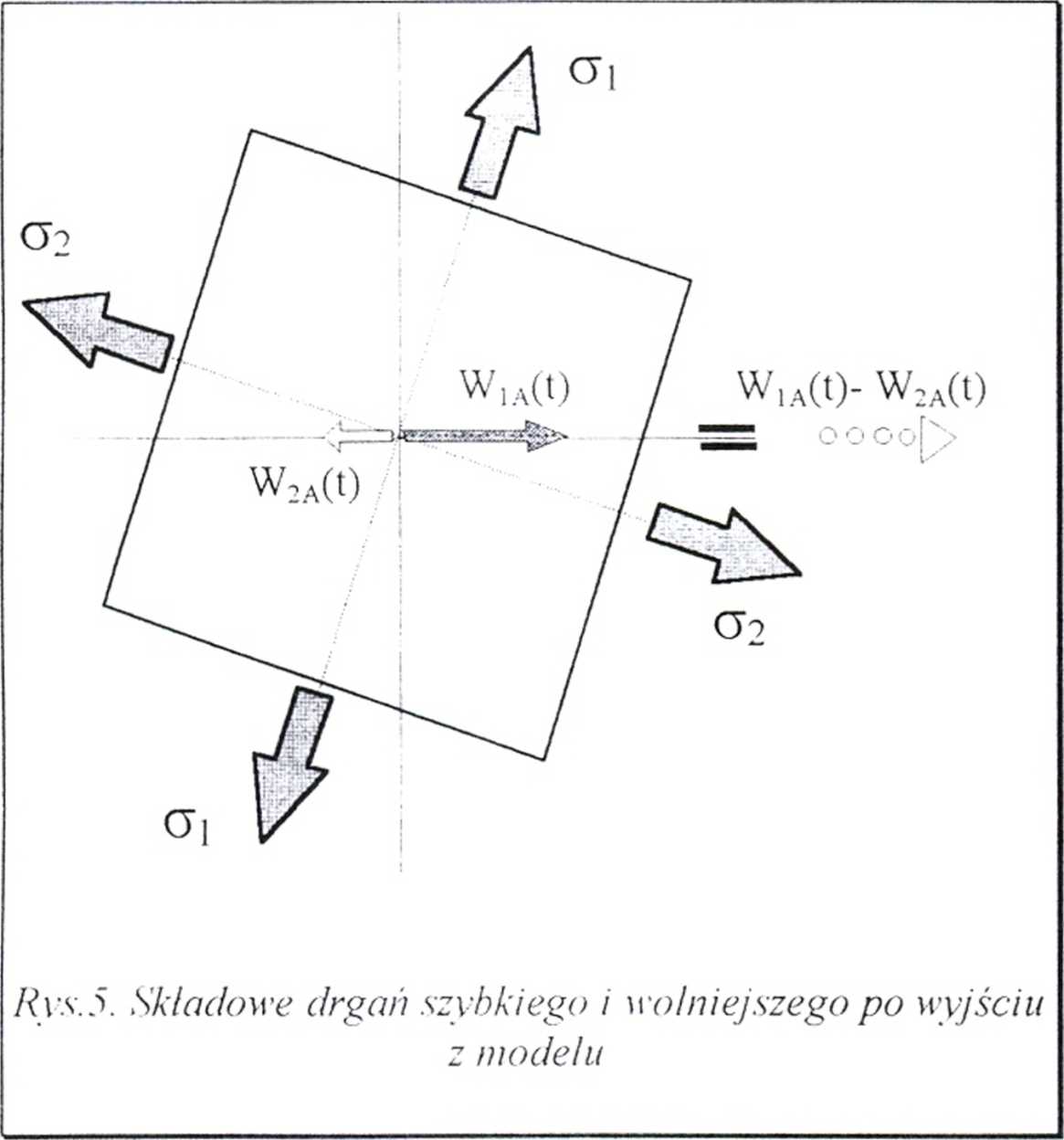
Strumień ten (a więc i jasność omawianej mikrokostki z rys.4), dla danego polaryskopu i danego materiału modelu zależy zatem wyłącznie od kąta a pomiędzy kierunkiem jednego z naprężeń głównych (p. rys.4) a płaszczyzną polaryzatora, oraz od wartości przesunięcia fazowego A drgań W_lA i W_2A

(rys.5) po wyjściu obu czół fal (szybszej i wolniejszej) z modelu. Po wyjściu z modelu obie fale propagują znowu z jednakowymi prędkościami, równymi prędkości światła w powietrzu.

U uważnego czytelnika powstanie niewątpliwie pytanie: jak to jest możliwe, że z fali drgającej (przed modelem) jedynie w płaszczyźnie pionowej (rys.3) powstało za modelem drganie w płaszczyźnie poziomej W_A(t) ?

Odpowiedź pośrednio mieści się w tekście powyżej i wynika z własności dwójłomności materiału modelu. Prócz tego nie należy zapominać, że istnieją także inne składowe drgań poza płaszczyzną A-A (rys.4), ale zostaną one wygaszone przy przejściu przez analizator⁴.

7

r