Transformacja Laplace'a w4
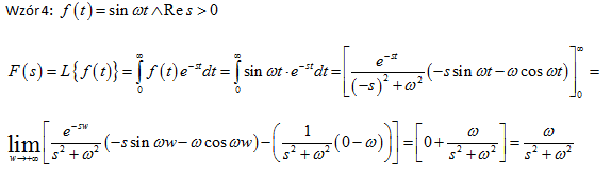
Wzór 4: / (?) = sin cot AR.es > O
OD 03
F (j) = L {/(t)} = \f{t) e~*dt = (* sin cot ■ e~stdt=
-a
(-s)‘ + o‘
(—5 sin ot — o cos cot)
_ ( 1 (-5 si n cow- o cos o\v) -1 ; — -; (O — o)
s2 + o2
|
co | ||
|
= |
Oh—=-j | |
|
' |
S2+&2_ |
s2 + o2
o
Wyszukiwarka
Podobne podstrony:
Transformacja Laplace a w3 Wzór-3:- f(t)= cos cot aRcs > 0[fl F(^) = L (/(0} = f f(t) e~"dt
Transformacja Laplace a w6 Wzór6: f(t) = cosh cot AR.es >
Transformacja Laplace a w2 Wzór 2: f{t I = e1 aRcs > Re <3 a-s1 s -a CD CD t a-s ~ cd r f
Zaliczenie ćwiczenia Zestaw 32 1. Rozwiązać przy pomocy transformat Laplace a równanie a) &nbs
7857994106598 Zdj (1 cie0441 Zestaw 32 1. Rozwiązać przy pomocy transformat Laplace a równanie a) &n
Tabela transformat Laplace a x(t) X(s) x(t) x(s) S(t) 1 (l-e-f-KO n s ■ (s + l)- 0+ 2).. .(s +
Transformacja Laplace a w7 Wzór7: /(?) = teat ARer > Rea /**($■) = l{ f(f)}= f f (?)e 5tdt = (&qu
Transformaty Laplace a x(t) X(t) x(t) X(t) S(t) 1 (l-e-f-KO n s ■ (s + l)- 0+ 2).. .(s +
skan0341 D2. Zastosowanie transformacji Laplace’a do rozwiązania równania dyfuzji jednowymiarowej(II
>Kaio automat, c:na >Kaio automat, c:na Zadanie 1. Wyznaczyć transformatę LaplaceTa funkcji
22884 skan0343 346 Zastosowanie transformacji Laplace’a C, = C(0,5) = Sf{c(0,0} =SE{cs} = A ponieważ
img119 cos x -f i sin o- f COS ar = ±(eł* + e-«) [sina- = - e~ix)
9 PRZEKSZTAŁCENIE LAPLACE’a str. 127 Tabela 8.1 Transformaty Laplace’a wybranych
PRZEKSZTAŁCENIE LAPLACE’a str. Tabela 8.1 Transformaty Laplace’a wybranych
3 (287) _ Grupa B Część 1 1. Co to jest transformata Laplace’a, w jakim celują sto
9oer> • cK W frwu; t>o Tabela 2. Wybrane transformaty Laplace’a
więcej podobnych podstron