DSCN1133 (2)

DME poprowadzonych odpowiednio do boków HI, FG i DE. Niech h_x, h₂. h₃ oznaczają długości wysokości trójkąta ABC opuszczonych na boki AB, BC, AC.

Trójkąty MI H, FGM i DEM są parami podobne, bo każdy z nich jest podobny do trójkąta ABC.

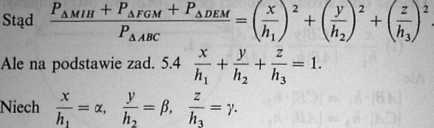
Zatem a + P + y = 1. Stąd

(a + P + y)² = 1 = a² + P² + y² + 2 a/? + 2ay + 2/fy, Teraz korzystając z zadania 1.7 mamy:

a² + p² > 2afi, a² + y² ^ 2ay i /?² + y² ^ 20y.

Po dodaniu tych nierówności stronami otrzymujemy: 2(a² + 0² + y²) ^ 2a.p + 2ay + 20y.

Ponieważ 2ocp + 2ay + 2/?y = 1 — (a² + /?² + y²), więc 2(a² + p² + y²)>l- (a² + j?² + y²).

Stąd a.² + P² + y²>

co oznacza, ze

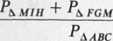
+ DEM

3

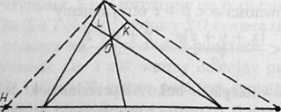
5.7. Przez wierzchołek C (rys. 5.7) trójkąta ABC kreślimy prostą CG\\BLoraz prostą CH\\AK.

<4

M

B

G

Rys. 5.7

Stosując twierdzenie Talesa lub rozpatrując odpowiednie trójkąty podobne, otrzymujemy

\AL\_\AB\    \M0\    | MB\

\LC\~\BG\' \0C\ || \BG\ ’ a stąd

\AL\ • |0C| • \MB\ = |AB| • |LC| • \M0\.

Stosując twierdzenie Talesa dla kątów: -tHBC i <//MC po przekształceniach otrzymujemy:

(2) |ieq • \mo\ • ja = \bk\ • |oq • mmi.

Mnożąc stronami równości (1) i (2), i przekształcając otrzymaną równość mamy \AM\ \BK\ |CL| _

|MB| |/cq |L4| ^L

5.8.    Korzystając z twierdzenia cosinusów mamy:

C a² = b² + c² — 2hc-cos<i4 < b² = a² + c² — 2ac• cos t c² = a² + B² — 2fló*cos<C.

Dodając powyższe równości stronami, otrzymujemy:

1) a² + b² + c² = 2(nB • cos •£ C + Bc*cos<M + ac-cos^B).

Ale

cos<j:y4, cos*B. cos<Ce(-l; 1), zatem

C ab • cos < C < ab (2) < Bc-cos<y4 < bc (.ac*cos<B < ac,

więc uwzględniając (2) w równości 1) otrzymujemy a² + b² + c² < ab + bc + ac.

5.9.    Niech \AB\ = c, \AC\ — b, jBC\ = a, punkt D będzie środkiem wysokości, a punkt S środkiem boku AB. Wtedy stosując twierdzenie cosinusów otrzymamy:

|_C£). _ Vp(P - a)(P ~ b)(p - c)

5.10.    Trójkąty ABD i MAD są podobne,

123