DSCN1161

Teraz łatwo narysować szukany prostokąt. Jest nim prostokąt, którego jednym bokiem jest AB, a drugim połowa wysokości trójkąta A BE poprowadzona z wierzchołka E.

6.34. Wskazówka. Metodą opisaną w rozwiązaniu zadania 6.33 najpierw konstruujemy trójkąt ABE o polu danego czworokąta. Niech \AB\ = a \ niech wysokość trójkąta ABE opuszczona na bok AB ma długość h.

Jeśli długość boku szukanego kwadratu oznaczymy przez x, to

K² = ga-h, skąd x =

Oznacza to, że długość szukanego boku kwadratu jest średnią geometryczną połowy długości boku AB i wysokości trójkąta.

6.35. Wskazówka. Załóżmy, że zadanie zostało rozwiązane. Wówczas

(rys. 6.35) _D

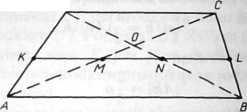
Rys. 6.35

AAKM-AADC,

AKDN~AABD.

więc

|JCAf| \AK\

' \DC\ \AD\ ’

2) 1*^N1 ’ \AB\ \AD\

Dzieląc stronami proporcję 1) i 2) po przekształceniach otrzymujemy równość \AB\ \AD\

' 2\DC\ \KD\ z której wynika konstrukcja.

Zadanie ma zawsze dwa rozwiązania. Drugie otrzymamy przez zamianę rolami podstaw AB i CD.

6.36. Niech \PB\ = x, \PA| = y. Na podstawie twierdzenia o stycznej i siecznej mamy:

\AP\² = \PC\-\PB\, (rys. 6.36) czyli

y² = (x + 2r)x.

Z drugiej strony, z treści zadania wynika, że x + y = a.

mamy więc układ równań.	A
Ix + y = a
\y^2 - x^2 = 2rx.	f ^s /
Skąd otrzymujemy
a^1
^X~2(a + ry
Z proporcji	Rys. 6.36

x a

a 2 (a + r)

widać, że szukany odcinek jest czwartym proporcjonalnym do odcinków o długościach a, a. 2(a + r). Zadanie ma zawsze dwa rozwiązania, po obu stronach punktu A.

6.37.    Jeżeli długość promienia danego okręgu jest R, zaś szukanego r, to r = (2^/3 — 3)R. Środki małych okręgów są wierzchołkami trójkąta równobocznego o boku 2r.

6.38.    Wskazówka. Narysujmy dowolną cięciwę BC i znajdźmy na niej punkt S dzielący ją na dwie części w stosunku 1:3, tzn. |BS|: |SC| =1:3 (rys. 6.38). Obróćmy punkt S dokoła punktu O o taki kąt a, że O_a (S)eO/ł. Dokonując obrotu cięciwy BC dokoła punktu O o kąt a, otrzymujemy cięciwę B'C' spełniającą warunki zadania.

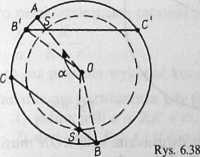
Z powyższego wynika, że zadanie ma nieskończenie wiele rozwiązań.

6.39. Wskazówka. Załóżmy, że skonstruowaliśmy prostą k oraz że punkt 5 jest środkiem odcinka AB.

179