DSCF6556

68

Ar = 0;

d²T d²T j d^^{i +} dy²~°

I

w pewnym obszarze (w naszym przykładzie jest to powierzchnia płyty, nie licząc krawędzi) oraz

T=f(x,y)    I

na granicy obszaru (w przykładzie znane są temperatury (wzór 2) w węzłach leżących na krawędzi płyty).

Równanie 1, będące szczególnym przypadkiem równania Poissone’a, nazywa się równaniem Laplace’a*. Omówmy teraz krótko metodę jego rozwiązania numerycznego. Zauważmy, że badając temperatury w węzłach próbujemy znaleźć wartości funkcji dwu zmiennych T (x, y) dla wartości zmiennych, różniących się skokowo o wielokrotność pewnego przyrostu elementarnego h (w naszym przykładzie h = 1). Spróbujmy zapisać równanie 1 w przybliżonej postaci, umożliwiającej wykorzystanie numerycznej metody rozwiązania. Przypomnijmy, że pochodna funkcji jednej zmiennej u(x), którą oznaczać będziemy przez u_x, obliczona w punkcie x₀, określona jest jako granica ilorazu różnicowego przy dążącym do 0 przyroście h zmiennej niezależnej x:

U,(kó) i lim

a-o

u(xo + h)~ u(x₀) h

(3)

Oczywiście w przypadku obliczania pochodnej przy użyciu maszyny cyfrowej h nie może być „nieskończenie” małe, lecz zawsze skończone i w związku z tym pochodną zastępuje iloraz różnicowy. Wyrażenie 3, uogólnione dla przypadku funkcji dwu zmiennych oraz drugich pochodnych ^u*x i ^uyy (proste wyprowadzenie można znaleźć w podręcznikach dotyczących metod numerycznych, np. [12]), ma postać:

I ..X u(x₀ + h,y₀)-M^x0,y₀) + u(x₀-h,y_o)

^Mxxl-*0» ro) —    ------- t'“/

f, (r ,rl - iii yo-h)- 2 u(x₀, y₀) + u(x₀, y_a + h)

Wo.W    - —pg---    (4b)

W naszym przypadku h= 1, dzięki czemu ostatnie wzory uzyskują prostszą formę:

Por. wstęp do ćw. E-l.

«xx(i,j) = u(i + 1,/) -2u(i,j) + u(i- l,j) =

(5a)

“»(*'. 7) = ^U(‘J - I - 2u(i,j) + u(i,j + 1) =

⁼ ui.j- i^— 2U|,j + U(j+1

(5b)

Podstawiając 5a i 5b do 1 otrzymamy przybliżoną formę równania Laplace’a:

«i+1.1 i «I- l.j + Ul. j+Ssij i I - 4uj, j = 0

(6)

Wynika stąd, że wartość funkcji u w danym węźle o współrzędnych (i, j) jest równa średniej arytmetycznej z wartości w czterech sąsiednich węzłach (zakreskowane krążki na rys. 11):

^ul+1,i + Uj-ij + Ujj+ 1 + Uj j-1 4

(7)

Jest to wynik intuicyjnie oczekiwany, o prostej interpretacji geometrycznej - każdą gładką powierzchnię można w niezbyt dużym obszarze przybliżyć przez powierzchnię kuli. W naszym przykładzie wzór 7 wskazuje, że temperaturę w dowolnym węźle można znaleźć ze znajomości temperatur czterech sąsiednich węzłów. Tak więc np. w węźle o indeksach (4, 2) temperatura będzie równa średniej arytmetycznej z temperatur T_s>2,

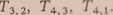
3. Schemat obliczeń

Temperatury w skrajnych punktach są znane (warunki brzegowe), dodatkowo należy wstępnie zadać dowolne temperatury w pozostałych węzłach: niech będą to temperatury T_lt] = 0 (i = 1, ..., 6; j = 1, ..., 6). Obliczenia zaczniemy od punktu (1, 1), znajdując T_ltl:

7’i,i=^(T^,o.i + 7’₂,i + T_1i0 + T_1i2) — = ^(42 + 0 + 42 + 0) = 21

Następnie obliczamy T_2>1, wykorzystując „nową”, znalezioną przed chwilą, wartość Ti.i. Po wykonaniu podobnych obliczeń dla pozostałych węzłów (oczywiście nie licząc brzegowych) kończy się cykl nazywany