dupa0088

y =-= 78 min zl

10

Współczynnik zbieżności:

Y(y<-yf

4045,78

nm

= 0,146

informuje, że 14,6% zmienności obrotów w badanych sklepach nie jest wyjaśnione przez kształtowanie się wielkości zatrudnienia, będąc następstwem oddziaływania innych czynników. Wartość współczynnika niezbyt oddalona od 0 wskazuje, że funkcja dość dobrze opisuje rzeczywisty wpływ zatrudnienia na wielkość obrotów.

Współczynnik determinacji:

R^:(y.x) = 1 -tp ²(yx) = 1-0,146 = 0,854

oznacza, że 85% zmienności obrotów w badanych sklepach jest wyjaśnione kształtowaniem się wielkości zatrudnienia.

Współczynnik korelacji:

R(yx) = yj\-(p²(yx) =    -0,146 = 0,924 świadczy o dość dużej sile współzależności między obrotami i zatrudnieniem i jest równy współczynnikowi korelacji Pcarsona obliczonemu w P3.5.

B. Oceniamy dopasowanie funkcji o postaci ,v₍ = 1,33 + 0,124y_i (1*3.12), opisującej wpływ wielkości obrotów' (y,) na liczbę zatrudnionych (.v,).

X,	y,	*1	(•W/)	(*(-*()	(^vf ~^xt)
23	149	19,8	3,2	10,24	12	144
4	35	5,7	-1.7	2,89	-7	49
12	69	9,9	2,1	4,41	1	1
3	33	5,4	-2,4	5,76	-8	64
17	119	16,1	0,9	0,81	6	36
2	6	2,1	-0,1	0,01	-9	81
21	176	23,2	-2,2	4,84	10	100
9	98	13,5	-4,5	20,25	-2	4
7	48	7.3	-0,3	0,09	-4	16
12	47	7.2	4.8	23.04	1	1
110	780	X	X	72.34	O	496

Współczynnik zbieżności:

R²(\y) = 1 -<p²(xy) = 1 - 0,146 = 0,854

Współczynnik korelacji:

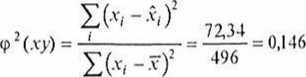
Współczynnik determinacji:

R(xy) = VH²(xy) = 0,924

Interpretacja obliczonych charakterystyk liczbowych taka sama jak poprzednio.

Jak mogliśmy zauważyć, analizując wyniki obliczeń wykonanych w P3.17, współczynniki zbieżności, współczynniki determinacji i współczynniki korelacji dla obu funkcji liniowych są takie same, o czym pisano przy omawianiu współczynnika korelacji Pcarsona. A zatem nawet wtedy, gdy mamy do czynienia z liniowym związkiem dwustronnym i szacujemy parametry obu funkcji regresji omówione wyżej miary wystarczy obliczyć tylko dla jednej funkcji.

Jeżeli analizujemy związek dwóch cech na podstawie informacji zapisanych w tablicy korelacyjnej, chcąc ocenić regresję, posłużymy się wzorami pośrednimi (3.30 - 3.33).

1’3.18. Obliczanie metodą pośrednią parametrów funkcji regresji opisujących powiązania między stawką zaszeregowania (x,) oraz liczbą dni absencji chorobowej (y,) w zbiorowości pracownic pewnego zakładu w maju 1988 r.

W P3.6 obliczono r(xy) = -0,581. x = 82 z.l/1 rg, y = 7 dni,

.v(.r) = 6.59 z.l/1 rg, s(y) = 3.89 dni.

A. Parametry funkcji opisującej wpływ stawki zaszeregowania (x,) na liczbę dni absencji (y,):

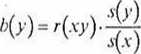
3 89

= _o,581. — = -0,34 6,59

a(y) =y- b(y)-x = 7 - (-0,34) • 82 = 34,88

Funkcja ma postać fy = 34,88 -0,34.v₍, a współczynnik regresji informuje, że

zwiększenie stawki zaszeregowania o 10 z.l powoduje spadek absencji chorobowej o 3,4 dni.

171