dupa0091

pokazuje średnią różnicę pomiędzy zaobserwowanymi wartościami zmiennej Y i krzywą regresji.

Współczynnik zbieżności (indctcrminacji):

<p²0*) =

(3.61)

IOW,)² I h-yf

i infonnujc, jaka część zmienności Y nic została wyjaśniona wpływem X określonym aproksymowaną funkcją.

Współczynnik determinacji:

R\vx) = 1 - <p²(yx)    (3.62)

pokazuje, jaka część zmienności Y została wyjaśniona oddziaływaniem X określonym funkcją regresji.

Indeks korelacji:

I (*-■&)*

R{yx) = VI - 9² O'*)

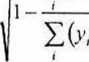
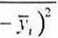
(3.63)

jest miarą korelacji krzywoliniowej. Współczynnik ten przejmuje wartości z przedziału (0;1), a zatem pokazuje silę skorelowania zmiennej zależnej Y ze zmienną niezależną A", nic informując o kierunku korelacji.

P3.20. Obliczanie parametrów krzywoliniowych funkcji regresji opisujących wpływ kolejnych dni tygodnia (.v,) na liczbę wypadków przy pracy (y,), jakie wydtirzyly się w' 1990 r. w pewnym dużym zakładzie przemysłowym (źródło: dane umowne):

Dzień tygodnia	^xi	1	2	3	4	5
Liczba wypadków	Xi_	73	56	40	34	32

	80 j
	70 --
S5	60 --
rz n	50 --
£ ✓	40 •-
*22 o	30 --
	20 --
	10 --

12    3    4    5

dziuń tygodnia

Rys. 3.6. Wykres korelacyjny liczby wypadków względem dni tygodnia

A. Aproksymujemy funkcję potęgową y_t = a ■ x, . Funkcję przekształcamy w postać liniową: log v_y = loga + b- logx,, a następnie wykonujemy obliczenia niezbędne do zapisania układu równań normalnych (3.52).

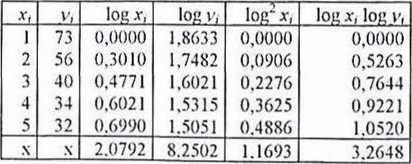
Obliczamy parametry funkcji adaptując wzory (3.25 i 3.26) na parametry funkcji liniowej:

"Z log logy, - Z log Y log

_b = __i_■    _ 5-3.2648-2,0792-8.2502

5-1,1693- (2.0792)³

■ = -0,545

«Z^loe² *. - Z^|og*.

'    \ ‘ J

Z^log.V, -*Z log Ar,

logu = —_,    8.2502-(-0,545)-2,0792

= 1.8767 ; a = 75,2835

177