dupa0096

należącymi do przedziału (0;1), uwzględniają rozmiary tablicy oraz liczbę obserwacji. Jednakże przed przystąpieniem do pomiaru siły współzależności cech warto odpowiedzieć sobie na pytanie, czy związek między nimi jest statystycznie istotny^{1 2}. Współzależność ocenimy jako istotną z prawdopodobieństwem popełnienia błędu 0,05 wtedy, gdy obliczona statystyka X będzie nie mniejsza niż

podane niżej¹⁰ przy danej wielkości (k- !)•(/ - 1):

(k-\)(l-\)	Xn.ns	(*-l)(/-D	2^0.05
1	3,841	11	19,675
2	5,991	12	21,026
3	7,814	13	22,362
4	9,488	14	23,685
5	11,070	15	24,996
6	12,592	16	26,296
7	14,067	17	27,587
8	15,507	18	28,869
9	16,919	19	30,144
10	18.307	20	31.410

Przedstawiamy trzy współczynniki kontyngcncji, najczęściej omawiane w literaturze, zastrzegając jednocześnie, że każdy z nich daje nieco odmienne wyniki. Współczynniki te mogą być stosowane, gdy obie cechy są jakościowe, gdy jedna jest ilościowa, a druga jakościowa, a także wtedy, gdy obie cechy są ilościowe. Współczynniki oparte są na warunkowych rozkładach liczebności, a zatem mogą być traktowane jako miara związku stochastycznego. Ich wartość równa 0 świadczy o stochastycznej niezależności cech, a im bardziej oddala się ona od 0, tym związek jest silniejszy, czyli badane cechy są z sobą skojarzone.

r=

v^wV(*^_1H^/-1)

Współczynnik FCramera

(3.66)

V =

yzz• min(/r — 1 ; /-l) Współczynnik kontyngencji C Pearsona:

^c=J£

(3.67)

(3.68)

Górna granica tego współczynnika zależy od liczby kolumn i wierszy, dlatego przy ocenie siły współzależności wprowadza się korektę, polegającą na podzieleniu C przez maksymalną wartość współczynnika dla danych rozmiarów tablicy.

C

m.ix

C

gdy k*l

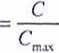
gdy k=l    (3.69)

(3.70)

Stąd też:

(3.71)

P3.22. Obliczanie współczynników kontyngencji dla oceny siły współzależności pomiędzy działem gospodarki i następstwami wypadków przy pracy. W P3.21 obliczono £ = 141,45 , z tablicy składającej się z k = 3 wierszy i / = 4 kolumn , n= 1353.

A. Obliczona statystyka z²jest większa od ^o.os przy (k - l)-(/ - 1) = 6. a zatem związek między działem gospodarki i następstwami wypadków jest statystycznie istotny.

i

187

1

   Pojęcie zostało wyjaśniono w punkcie 3.4.

2

   Wartości graniczne (tzw. wartości krytyczne) statystyki X przytoczono za R.Zieliński, Tablice statystyczne. Warszawa, PWN 1972, s.l 15.

186