dupa0104

bądź też możemy zastosować zmienną podstawę porównań, odnosząc poziom zjawiska w okresie badanym (y,) do poziomu w okresie bezpośrednio poprzedzającym (y_M) i otrzymując tym sposobem indeksy łańcuchowe.

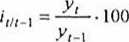
(4.3)

Indeksy najczęściej wyrażamy w procentach.

Jednym z częściej stosowanych mierników dynamiki jest tempo przyrostu, czyli względny przyrost łańcuchowy, zwany krótko tempem.

Tempo zapisujemy jako stosunek przyrostu absolutnego (zly,) do wielkości zjawiska z poprzedniego okresu.

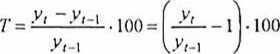
(4.4)

Po pomnożeniu przez 100 otrzymujemy przyrost wyrażony w procentach. Jeżeli zamiast przyrostu występuje spadek zjawiska, to tempo będzie wielkością ujemną.

Porównując wskaźnik tempa przyrostu z łańcuchowym wskaźnikiem dynamiki, dostrzegamy pewne związki matematyczne, mianowicie tempo równa się indeksowi łańcuchowemu pomniejszonemu o 1 (lub 100 w wyrażeniu procentowym), indeks łańcuchowy zaś równa się 1 (100) plus tempo.

Technikę liczenia wskaźników dynamiki i tempa prześledzimy na przykładzie szeregów czasowych przedstawionych w P4.1 i P4.2,

1992:

P4.5. Oblic/anic wskaźników dynamiki i tempa dla szeregów przedstawiających liczbę abonentów telefonicznych oraz liczbę urodzeń żywycIr w Polsce w latach 1982—

A. Liczba abonentów telefonicznych w tvs. w Polsce (w,).

Lala	y>	Indeksy jednopodstawowe (rok 1982= 100)	Indeksy łańcuchowe (rok poprzedni = 100)	Tempo w %
1982	2 109	100,0	-	_
1983	2 217	105,1	105,1	5.1
1984	2 349	111,4	106,0	6.0
1985	2 480	117,6	105,6	5,6
1986	2 625	124,5	105,9	5,9
1987	2 774	131,5	105,7	5,7
1988	2 953	140,0	106,5	6,5
1989	3 121	148,0	105,7	5.7
1990	3 293	156,1	105,5	5,5
1991	3 565	169,0	108,3	8,3
1992	3 938	186.7	110,5	10.5

li. Urodzenia żywe w tvs. w Polsce (w,).

Lata	y,	1 ndeksy jednopodstawowe (rok 1982 = 100)	Indeksy łańcuchowe (rok poprzedni = 100)	Tempo w %
1982	702.4	100,0	—	_
1983	720,8	102.6	102,6	2.6
1984	699,0	99,5	97.0	-3.0
1985	677.6	96,5	96.9	-3.1
1986	634.7	90,4	93.7	-6,3
1987	605,5	86.2	95.4	-4,6
1988	587,7	83,7	97.1	-2,9
1989	562,5	80,1	95.7	-4,3
1990	545,8	77,1	97,0	-3,0
1991	546,0	77.7	100,0	0.0
1992	513.6	73.1	94.1	-5.9

Obserwując szeregi indeksów jednopodstnwowycli. dostrzegamy ogólną tendencję zmian w odniesieniu do stanu w 1982 r.. który został przyjęty jako podstawa porównań. Liczba abonentów telefonicznych w kolejnych lalach była relatywnie coraz większa w stosunku do okresu podstawowego i w 1992 r. stanowiła ona 186,7% stanu z 1982 r., czyli była o 86,7% większa. Natomiast liczba urodzeń zmniejszała się w kolejnych lalach, stanowiąc w 1992 r. 73,1% liczby urodzeń w 1982 r.. czyli była o 26.9% niższa. Indeksy łańcuchowe pokazują względne zmiany z roku na rok. Wynika z nich, że największe przyrosty względne liczby abonentów' wystąpiły w 1991 r. i 1992 r. Z kolei najsilniejszy spadek urodzeń odnotowano w 1986 r. oraz 1992 r.

Między indeksami jednopodstawowymi i łańcuchowymi występują związki matematyczne, leli znajomość jest przydatna w sytuacjach, gdy nic

203