freakpp087

172

8.4. Zastosowanie metody różnic skończonych do ustalonego, dwuwymiarowego przewodzenia ciepła

= 0.

(8.29)

Podczas ustalonego przewodzenia ciepła w ciałach stałych człon

Rówmmie Kirchhoffa-Fouriera przyjmuje wtedy postać:

_aV²T + ^- = 0

pc

Wstawiając w równaniu (8.29) zamiast operatora V²T zależność (8.7) i przyjmując jednocześnie 8_xy = 0, otrzymuje się:

Ti+l,j 2Tjj+Tj_jj ^ Tj,j+l 2Ty + Tjj_]

(^Ay)'

+ ^ = 0 pc

(8.30)

Jeżeli Ax = Ay = Al, to równanie (8.30) sprowadza się do postaci:

^Ti+l,j ~ ^4Ti,j ^{+ T}i-l,j ^{+ T}i,j+1 ^{+ T}i,j-1 (Al)²

+ ^ = 0 pc

(8.31)

Warunki brzegowe określa się podobnie jak poprzednio, przyjmując jednocześnie, w bilansach energii, że moc akumulacji AH = 0.

8.5. Przykład

Dla przykładu zostanie rozpatrzony proces ogrzewania długiego pręta o przekroju prostokątnym 2H x 2L, rys. 8.8. Temperatura początkowa wynosi Tj, a temperatura otaczającego płynu T_f. Współczynniki przejmowania ciepła aj, a₂, a₃ nie ulegają zmianie w czasie ogrzewania pręta.

Pole temperatury będzie symetryczne względem osi y, czyli dla współrzęd-

0T

nej x - 0, — = 0. Oznacza to, że w obliczeniach wystarczy rozpatrywać tylko dx

połowę pręta. W tym przypadku symetria pola temperatury pozwala na zmniejszenie liczby równań różnicowych o połowę. Do aproksymacji pochodnej tern-

peratury względem czasu zostanie zastosowany iloraz różnicowy wsteczny (8.10). Dla wszystkich węzłów, oprócz jednego oznaczonego numerem (2,2), należy ułożyć równania różnicowe na podstawie bilansu mocy. Opierając się na wzorze (8.14), można zapisać równanie różnicowe w węźle (2,2) natępująco:

^T2,2,k-1 = A*⁷⁰

^-Fl,2,k +1 ⁴ +

AFo

-T-

3,2, k ^-T2,l,k ~^T2,3,k

Al    “3

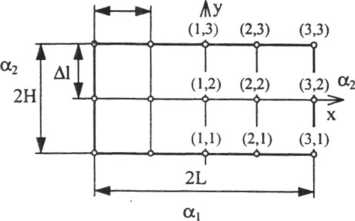
Rys. 8.8. Podział pręta siatką różnicową

(8.32)

Bilans energii w elemencie ABG(1,1), rys. 8.9, obejmującym węzeł (1,1) jest następujący:

k “^Tl,l,k)^ = (^Tl,l,k ^_Tl,2,k)—

“iy(Tf-T_uk) + (T₂,_1>

(8.33)

_pc(^AI)^{2 T}l,l.k ~^Tl,l,k-l _t ⁴ *k ^—tk—1

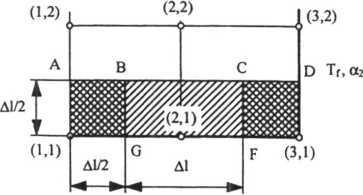
T_f> a,

Rys. 8.9. Elementy bilansowe