HPIM5127

Natomiast między kątami obrotu obydwu walów łączonych sprzęgłem istnieje zależność

(1.27)

tg ?>2 = tgtpicoso

Przy kącie obrotu <pi = 0 oraz <pi = 180° prędkość kątowa wału napędzanego osiąga wartość maksymalną

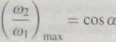
(1.28)

Zmiany prędkości kątowej wału napędzającego i napędzanego w zależności od kąta między łączonymi wałami i drogi kątowej wału napędowego <pi przedstawiono na rys. 1.14.

Prędkość wału napędzanego zmienia się okresowo, przy czym okres tej zmienności jest połową czasu jednego obrotu. Taka niejednostajność prędkości kątowych jest do przyjęcia w maszynach z wałami wolnoobrotowymi, przy małych masach obracających się elementów. Jest to ważne ze względu na przyspieszenia kątowe działające na człony sprzęgła. Przyspieszenie kątowe członu napędzanego ma postać

£|

cos a

+ 6)1

sin^-a cos a sin 2<pi

1 - sin~ a sin* <pi    (1 — sin ot sin <pi)“

gdzie £| - przyspieszenie kątowe członu napędzającego.

(1.29)

Jeżeli prędkość kątowa wału napędzającego o>i = const, to £| = 0 i wtedy

£2 = Q)|

sin² a cos a sin 2ę>i (1 - sin² a sin² <pi )²

(1.30)

Niejednostajność ruchu obrotowego członów sprzęgła kątowego można usunąć przez:

- zastosowanie sprzęgła kątowego podwojonego (rys. 1.15). Wałek pośredni w tym rozwiązaniu powinien mieć ramiona krzyża na obydwu końcach w jednej płaszczyźnie. Kąty ct| między wałkiem napędzającym a pośrednim i «2 między pośrednim a wałem napędzanym powinny być jednakowe. Wałek pośredni ma prędkość obrotową zmienną; przy bardzo dużych prędkościach obrotowych jest to zjawisko niekorzystne, gdyż może być powodem powstawania drgań tego wału.

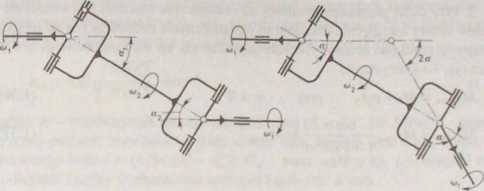
RYS. 1.15. Sprzęgło kątowe z wałkiem pośrednim

- zastosowanie sprzęgła kulowego (rys. 1.15 lub 1.18, 1.19). Uzyskuje się wtedy jednostajną prędkość obrotową na wale napędzanym a>i/a>2 = 1. Moment obrotowy, jaki przenosi sprzęgło kątowe pojedyncze (na wale napędzanym), łączące dwa wały, które są odchylone względem siebie o kąt a (patrz rys. 1.13), ma postać

M_a ~ cos a

(131)

Moment obrotowy na wale napędzanym (biernym) wynosi

(1.32)

a przy kątach <p\ = 0 oraz <p\ = n

cos a

(1.33)

Maksymalną siłę działającą na krzyżak (patrz rys. 1.13) można zapisać wzorem

„ M_pmax

*inax —

(1.34)

gdzie

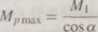
(135)

Przez moment na wale napędzającym M \ rozumie się moment obrotowy doprowadzany do sprzęgła przy stałej prędkości kątowej (<U| = const).

Obciążenie krzyża i widełek sprzęgła kątowego jest uzależnione od warunków jego pracy i tak:

I. Przy małej prędkości obrotowej P„_Wx momenty M_limax, A/2ma* określa się zgodnie ze wzorami (1.33), (1.34) i (1.35), przyjmując kąt odchylenia osi łączonych wałów a = 0 (przy którym obciążenia osiągają maksimum).

25