CCF20090421001 (2)

r

M i %>-■

m

'

■^!nf^V

i

Zależności między kątami a, p, y

Symetrii obrotowa:    ;

^ Jeśli występuje jedna oś obrotu wskazuje ona kierunek wyróżniony (uprzywilejowany), a pozostałe dwie osie są do hiej prostopadle np.

2y (Y); 3, -3,3m (Z); 4, -4, 4/m (Z); 6, 6rara (Z)

Wyjątkiem jest grupa punktowa mm2, w której brak kierunku wyróżnionego, a osi dwukrotne? przypisuję sie kierunek Z (2z)

=z> Gdy występuje więcej niż jedna oś obrotu kierunek wyróżniony jest zgodny z osia o najwyższej krotności    \

Np. 422,4/mra, -42m (Z 4z); 32 (Z 3z); 622, 6/mmm (Z 6z)

=> Jeśli występuje kilka osi obrotu o identycznych krotnościach to brak kierunku wyróżnionego, osiom o najwyższej krotności przypisuje się kierunki osi układu, zaś kąty między osiami są prostopadłe Np. 222, mmra (XYZ 2x2y2z); 432, -43m (XYZ 4x4y4z)

6. A-R\fcixc2\fe-?irci    i    7

Brak symetrii obrotowej:

=o Jeśli nie występuje oś obrotu, a jedynie płaszczyzna odbicia kierunek wyróżniony jest prostopadły do tei płaszczyzny (zwyczajowo jest to kierunek Y), a pozostałe kierunki są prostopadłe do osi wyróżnionej; m (Y my)

=3 Gdy nie występuje oś obrotu, ani płaszczyzna odbicia Diak

kierunku wyróżnionego, a wzajemne ustawienie osi jest dowolne: Np. 1, -1

Wartości kątów między osiami układu X, Y, Z (cl p, y), gdy osie te nie są prostopadłe, wynikają z krotności występujących osi obrotu

Ł AJt)C*r.xyt-Krc£

symetria	kierunek wyróżniony	kąty między osiami układu
1	*	dowosne ■
2 (2.)	Y	o=y=90
4 (4,)	^2	a=p=30^;
6 (6,)	^2	a=ji=90^3
3 (3.) 2 |
2 22 (2,2,2,)	-	a=p=,=S0^1
4 4 4 (4,4,4,)	'	, u=p-,=S0= ,

’ sjm&oi oznzcia .wartość c

a w stcsjnKu co 90⁵' (nie m_us; o>ć 50⁼)

i

i

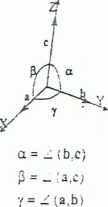
Zależności między siaiymi a, b, c

Wartości kątów miedzy osiami układu X, Y, Z (a, g, f). gdy osie ic nie są prostopadle, wynikają z krotności osi obrotu. Podobnie można wyprowadzić związki między długościami pertoaow ą, b c

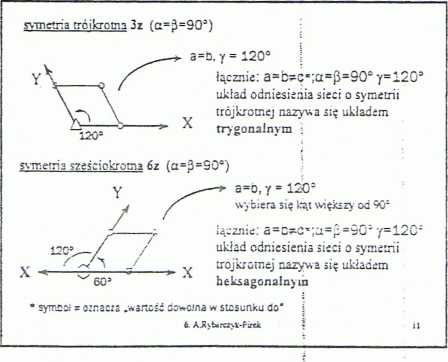
np. svrr.err.a eziero^-cma -Iz (a=|3=90‘)

a-o. y = 30¹

łącznie: a-C-c*:ct=p-,'=9G"

układ odniesienia sieci o r; rucini czterokrotnej nar,w i r;ę „ctioem tetragonalnym

aec.pe 90‘*

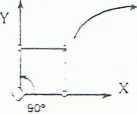
symetria dwukrotna 2y (a=7«90*)

symetria 2x 2y Iz

2y =5 ć-d^c*; a-/=90^d^j3**

2x => a-b?c*; (3=7=90°^a*

2z =e> 3=0^0'; a=i3=S0^c^ v*

symetria Ax 4y 4z

4z w a=D^c; a=p-/-9G^&

4x =» b=c^a; a=p=7=S0"

4y => 5=C^D; ct=p=y=90³

;a=y=SGⁱ^P* układ odniesienia sieci o symetrii dwukrotnej nazywa się układem jednoskośnym

łącznie; a;=bi=c^x;a=p=Y=90³ układ odniesienia sseci nary w a się

łącznie; 5=b=c ;a=p=y=9Q^c układ odniesienia sieci nazywa się układem regularny ra

—

■    Hf!

. gggii Ę ■- ■

-

2