CCF20090604002

symetria obrotowa	kier. wyróż.	ograniczenia na stałe sieciowe	układ	grupy punktowe
1	-	a*b=ic a^p?^90^o	trójskośny	1.-1
C\T CM	Y	a^b^c a=y=90°^p	jednoskośny	2, m, 2/m
222 (2,2.2,)	-	a^b^c a=p=y=90°	rombowy	222, mm2, mmm
4 (4,)	Z	a=b^c a=p=y=90°	tetragonalny	4, -4, 4/m, 4mm, 4/mmm, 422, -42m
6 (6Z)	Z	a=b*c a=P=90° y=120°	heksagonalny	6. -6, 6/m, 6mm, 6/mmm, 622, -62m
3 (3,) <3,„>	Z [111]	a=b*c a=p=90° y=120° a=b=c a=p=y^90°^120°	trygonalny w osiach heksagonalnych w osiach romboedrycznych	3. -3, 3m, 32, -3m
4 4 4 (4,4,4,) lub 3,„ 3.1M 3,.„ 3,,.,	”	a=b=c a=p=y=90° 9. A.Rybarczyk	regularny >irek	23. m-3, 432, -43m, m-3m 13

Układ trygonalny

O przynależności sieci do układu trygonalnego stanowi obecność symetrii trójkrotnej. Osi trójkrotnej w sieciach przestrzennych można przypisać kierunek na dwa sposoby:

z '

kierunek jednej z osi układu - zwyczajowo kierunek Z

=s> układ trygonalny w osiach heksagonalnych

identyczne zależności jak w układzie heksagonalnym

kierunek przekątnej pomiędzy trzema osiami układu - kierunek [111]

=> układ trygonalny w osiach romboedrycznych

od nazwy bryły jaką stanowi komórka elementarna (romboedr), jeśliby a=p=y=90° byłby to układ regularny

9. A Rybarczyk-Pirck

=b*c a=p=90° y=120°

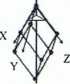
a=b=c a=p=y*90°*120°

W nomenklaturze grup punktowych istnieje system pozycyjny każda pozycja odnosi się do ściśle określonego kierunku, zależnie od rozpatrywanego układu krystalograficznego

układ krystalograficzny	pozycje i kierunki			przykładowe grupy
trójskośny				1
jednoskośny	Y (kierunek wyróżniony)			2.2/m
rombowy	X	Y	Z	222, mm2, mmm
tetragonalny heksagonalny trygonalny	z (kierunek wyróżniony)	X (Y)	li [110] przekątne podstawy komórki	4, 4mm, 422, -6,6/mmm, 3m, 32, -3m
regularny	X (Y,Z)	11(111] przekątne przestrzenne komórki	II [HO] przekątne podstawy komórki	23,-43m,m-3m

9. A.Rybarczyk-Pirck