CCF20090604001 (2)

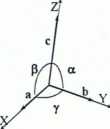
Zależności między kątami a, P, y
Symetria obrotowa:		Brak symetrii obrotowej:
=> Jeśli występuję jedna oś obrotu wskazuje ona kierunek wyróżniony		=> Jeśli nie występuje oś obrotu, a jedynie płaszczyzna odbicia
(uprzywilejowany), a pozostałe dwie osie są do niej prostopadłe np.		kierunek wyróżniony iest prostopadły do tei płaszczyzny
2y (Y); 3, -3,3m (Z); 4, -4,4/m (Z); 6,6mm (Z)		(zwyczajowo jest to kierunek Y), a pozostałe kierunki są prostopadłe
Wyjątkiem iest grupa punktowa mm2. w którei brak kierunku wyróżnionego, a osi dwukrotnej przypisuje sie kierunek Z (2z)		do osi wyróżnionej: m (Y my)
=> Gdy występuję wiecei niż iedna oś obrotu kierunek wyróżniony iest		=> Gdy nie występuje oś obrotu, ani płaszczyzna odbicia brak kierunku wyróżnionego, a wzaiemne ustawienie osi iest dowolne:
zgodny z osia o najwyższej krotności		Np. 1,-1 zj
Np. 422,4/mmm, -42m (Z 4z); 32 (Z 3z); 622,6/mmm (Z 6z)		Wartości kątów między osiami /
=> Jeśli występuję kilka osi obrotu o identycznych krotnościach to brak kierunku wyróżnionego, osiom o najwyższej krotności przypisuje się kierunki osi układu, zaś kąty między osiami są prostopadłe Np. 222, mmm (XYZ 2x2y2z); 432, -43m (XYZ 4x4y4z)		układu X, Y, Z (ot, P, y), ^c\ gdy osie te nie są prostopadłe, \ ^a wynikają z krotności ------ występujących osi obrotu Y
9. A.Rybarczyk-Pirek 7		9. A.Rybarczyk-Pirek 8

symetria obrotowa	kierunek wyróżniony	kąty między osiami układu
1	-	dowolne ustawienie osi* a^p^Y^90°
2 (2y) oraz my	Y	a=y=90
4 (4Z)	Z	a=p=90°
6 (6Z)	Z	a=p=90°
3 (3Z)	Z	a=p=90°
2 2 2 (2X 2y 2Z)	-	a=p=y=90°
4 4 4 (4x4y4z)	-	a=p=y=90°

a = Z (b,c) P = Z (a,c) y = Z (a,b)

* symbol *90° oznacza .wartość dowolna w stosunku do 90°" (nie musi być 90°)

9. A.Rybarczyk-Pirek

symetria tróikrotna 3z (a=P=90°)

Y

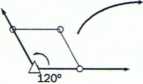
łącznie: a=b*c*;a=p=90° y=120 układ odniesienia sieci o symetrii trójkrotnej nazywa się układem ^ trygonalnym

a=b, y = 120°

symetria sześciokrotna 6z (a=P=90°)

X

a=b, y = 120°

wybiera się kąt większy od 90°

łącznie: a=b*c*;a=p=90° y=120° układ odniesienia sieci o symetrii trójkrotnej nazywa się układem heksagonalnym

* symbol * oznacza .wartość dowolna w stosunku do’

9. A.Rybarczyk-Pirek    11

Zależności między stałymi a, b, c

Wartości kątów między osiami układu X, Y, Z (ct, p, y), gdy osie te nie są prostopadłe, wynikają z krotności osi obrotu. Podobnie można wyprowadzić związki między długościami periodów a, b, c.

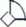
np. symetria czterokrotna 4z (a=3=90°)

Y

-o

o-

90°

a=b_t y = 90°

łącznie: a=b*c*;a=p=y=90°

X

układ odniesienia sieci o symetrii czterokrotnej nazywa się układem tetragonalnym

* symbol * oznacza .wartość dowolna w stosunku do’

9. A.Rybarczyk-Pirek    10

symetria dwukrotna 2v (a= y	=90°) ^—► a ^ c, p * 90°*
^v180° ^	łącznie: a^b^:?^ic*;a=y=90Vp*
	układ odniesienia sieci o symetrii dwukrotnej nazywa się układem
nie zdefiniowany trzeci kierunek (Z)	jednoskośnym
symetria 2x 2v 2z
2y => a#b«*; a=y=90^o:ip*	łącznie: a*b*c*;a=p=y=90°
2x =i> a*b*c*; p=y=90Va*	układ odniesienia sieci nazywa się
2z => a^b^c*; a=p=90V y*	układem rombowym
symetria 4x 4v 4z
4z => a=b^c; a=p=y=90°	łącznie: a=b=c ;a=p=y=90°
	układ odniesienia sieci nazywa się
4x => b=c*a; a=p=y=90°	układem regularnym
4y => a=c*b; a=P=y=90°
*	symbol * oznacza „wartość dowolna w stosunku do"
9. A.Rybarczyk-Pirek 12

2