CCF20090421002 (2)

symetria obrotowa	kier. wyroi.	ograniczenia na stałe sieciowe	układ	grupy punktowe
1-	-	a a5=ą*73=S0°	trójskoiny	1.-1
2 (2,)	Y	a*Ł^c a=Y=-90*=fl	jeancskcśny	2. m, 2/m
222 (2,2,2.)	•	apćs=c a=p=;=90^3	rombowy	222. mm2. mmm I
4 (4J	Z	a=fc^c a=p=y=90^s	tetraganainy	4. -4. 4/m. 4mm, 4/mmm. 422. -42m |
S (6J	^2	a=ł*=c a=0=5O^s y=12Q^a	heksagonalny	6, -o 6/m. 6mm. 6/mmm. 622. -62m |
3 (3,) (3 ,	^2 [mi	a=b=c a=p=S0^3y=120® a=b=c a=p=-pSQ^3^12C^0	trygonainy w cŁacn betsagońamyca * SŁScn romDoec.-ycccycn	3, -3. 3m. 32. -3m
4 4 4 (4,4 4.) 3,„ 3.,„ 3,.,, 3...,	_	a=b=c a=3=y=50^= ć. A JŁ\iar=rvv	regularny rirtk	23, m-3. 432. -43m, j m-3m ■3 ■

Układ trygonalny

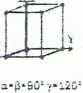
O przynależności sieci do układu trygonalnego Sianowi ubecnosc symetrii trój krotnej. Osi irójkromej w sieciach przestrzennych można przypisać kierunek na dwa sposoby:

Z {

kierunek jednej z osi układu - zwyczajowo kierunek Z

=5 układ cygonainy w osiach heksagonalnych

identyczne zależności jak w układzie heksagonalnym

a*D^c

kierunek przekątnej pomiędzy trzema osiami układu - kierunek [111]

=3- układ try gonalny w osiach romoedrycznych

cd nazwy bryły jaką stanowi komórka eierr.enuma iromcoedr), jeśliby c:=p=y=9G- byłby ic-układ regularny

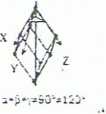
W nomenklaturze grup punktowych istnieje system pozycyjny każda pozycja odnosi się do ściśle określonego kierunku, zależnie od rozpatrywanego układu krystalograficznego

układ		jazycje i kierunki		prz> kładowe grapy
trójskosny				i
jećnoskosny	Y {koronek wyróżniony)			2.2/m
rombowy	X	I Y i	OZ	222, mm2.
tcijassna my	.^2	i OX (OY)	iidioj pr:eM'-re poestswy komórki	4. 4mm. 422. -6. ć/rr.mm, 3m. 32. -3m
	T;7ror .
trygonalny	i
rczulamy	X (Y. Z)	i nmi	ii f t »03 przekorne	23.-43m.m-3m
		I" «m£iu	komórki

Przypomnienie

Komórka elementarna - równoległoscian obejmujący najmniejszy powtarzający się penodycznie fragment sieci przestrzennej. Krawędzie komorki są zgodne z osiami układu krystalograficznego. Długości krawędzi komorki są równe długościom transiacji sieciowych a, b, c i tworzą między sobą kąty a, % f

-i? !

i |

i

Ci = Ul (b.C;

p = / (a.c) y = Z [a_:b)

Y

Kszialt komórek elementarnych w sieciach o różnej symetrii (w różnych ukiadach krystalograficznych)

r.-rarr^ sieci i ukhd j parametry komórki kr>suiogranczny I elementarnej		kształt komórki elementarnej
1 trójsknsny	n^r.90>
2, jednotkniny	a-r=SS“s(i	prostopadłościan w podstawie równołcgloboK
2,2,2, rombowy
4, tetragorudny	a=b^c e-^0-
6. heksagonalny 3. trygonsłny	a=j5-9C® y=120°
3,SI trygonalny	a=c-*=c a=^S0^120-
^4iVz regularny	a=b=c n=5>r=30-

komórki prymitywne

3

3?b?c

50³ trój skośna

5

a?b?c a * 90° * P

a*b;ec    o“b^c

a«0 = y»SO^a a-£-y-50^s

lerragonalna

a = b*c

a = 0 = 9O^a y=12Ct heksagonalna nygonalna

a » b ^a c

a = ji» ₇“S0=

nygonalna

SP

• t-J

'

■    - i ^ ■ ■    ■......

,    ■'i'*.-

&&

I