HPIM5171

Przyjmijmy następujące dwa założenia:

1)    współpracujące zarysy są w ciągłym kontakcie,

2)    zęby są nieodkształcalne.

Z założeń tych wynika, że rzuty prędkości V\ i v₂ na kierunek normalny do zarysów są sobie równe

vm = tta

co jest równoważne równości

v i cos yi = i*2 cos    (3,19)

Na podstawie wzorów (3.17), (3.18) i (3.19) mamy

a)i r\ cos yi — ft^ricos yi    (3.20)

Z rysunku 3.9 widać, że

cosy, = —

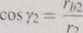
(3.21)

Po podstawieniu tych wyrażeń do związku (3.20) otrzymamy

©ifbl = <*>2/7*2

(3.22)

Ponieważ

>7*1 = r_H i cosa, r_b2 = r„ 2 cos a

(3.23)

zatem ze wzorów (3.21) i (3.22) wynika, że

©I ^rbl ^rw2

(3.24)

(Di fy i r*.|

Lewa strona wzoru (3.24) jest przełożeniem kinematycznym pary kół zębatych. Oznaczmy je symbolem /12. Mamy więc

©1    r*2

• it _

(02 r_H |

(3.25)

Wzór len wyraża podstawowe prawo zazębienia, zwane też prawem Wiłlisa, które można sformułować następująco:

W celu zapewnienia stałego przełożenia kinematycznego (/ = const) zarysy zębów powinny być takie, aby wspólna normalna N-N w dowolnym punkcie styku zębów B dzieliła odcinek 0\0i w stałym stosunku r_w2/r_w\.

Zarysy zębów spełniające ten warunek nazywamy zarysami sprzężonymi.

W czasie zazębienia punkt styku B zębów współpracujących przemieszcza się wzdłuż boku zęba. W kołach skonstruowanych zgodnie z podstawową zasadą zazębienia, niezależnie od położenia punktu B, normalna NN dzieli w stałym stosunku odcinek 0\0i. Przy stałej odległości osi oznacza to. że punkt toczny C nie zmienia swego położenia w czasie współpracy kół.

Zarysy zębów spełniające ten warunek współpracują zatem tak. aby okręgi o promieniach r_w\ i r_wi toczyły się po sobie bez poślizgu. Okręgi te nazywamy okręgami tocznymi, punkt C - biegunem zazębienia. a punkt B - punktem styku zębów (używa się również nazwy punkt przyporu).

Jeśli zgodnie z rys. 3.9 zauważymy, że odległość osi

IfeMIISipi    .    /-    (3.26)

to rozwiązując układ równań (3.25) i (3.26) względem r_H.| i r_Mo, otrzymamy wzory na promienie kół tocznych

=

I

1+/|2

fw2 = (Iw

<12

1 +<12

(3.27)

Dla zarysów sprzężonych przełożenie kinematyczne i u jest równe przełożeniu geometrycznemu u określonemu równością (3.15). Mamy więc

. fój Z2 tt>2 zj

Po uwzględnieniu tej równości we wzorach (3.27) otrzymamy

i =    —

-i +*2

(3.28)

Z2

r*2 = Ow——

Z\ +22

W rozważaniach nad prawem Willisa wykorzystano rzuty prędkości na kierunek normalnej N-N. W dalszej części zajmiemy się rzutami prędkości na kierunek stycznej T-T do zarysów zębów w punkcie przyporu B.

Różnica rzutów prędkości v\ i ł>2 na kierunek stycznej jest prędkością poślizgu współpracujących zarysów. Prędkość poślizgu oznaczymy symbolem v_s. Mamy zatem

i>j = h*2 — W|    '■■■:    (3.29)

Prędkość poślizgu u_v można łatwo wyznaczyć, rozpatrując ruch względny koła / względem koła 2. Ruch ten jest ruchem obrotowym wokół chwilowego środka obrotu, którym jest biegun zazębienia C. Prędkość kątowa tego ruchu jest prędkością względną koła / względem 2 i wynosi

(3.30)

O) 12 = 0)| + (02