HWScan00125

gdzie

h maksymalna wartość grubości skiby równa wysuwowi kola naczyniowego, m,    ^a

<P kąt obrotu naczynia liczony od pionowej przechodzącej prze? oś koła w stopniach.

4.6.2. Analiza równania grubości skiby

Otrzymane równanie (4.67) pokazuje, że zmienna wielkość grubości skiby jest funkcją kąta cp i jednocześnie zależy od geometrycznego parametru k_h, który zawarty jest tylko w drugim członie. Przebieg funkcji

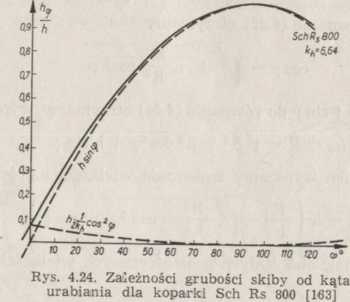
grubości skiby, wyrażonej częścią maksymalnej wielkości h dla koparki kołowej, pokazuje rys. 4.24. Grubość ta jest sumą obu zawartych w równaniu (4.67) członów. Wykresy pokazują, że wielkość grubości skiby prawie w całym przebiegu urabiania określona jest głównie przez wartość pierwszego składnika h sin cp.

Drugi składnik

h    ^cos2 V    (4.68)

wywiera nieznaczny wpływ na zmianę grubości skiby w zakresie kąta 120 !> cp > 10°. Tylko na początku przebiegu urabiania (9? <C 10^w). tj. przy grubości skiby 0    0,1 h, składnik (4.68) ma określony wpły^vV

na grubość skiby. Analiza równania (4.67) potwierdza to przypuszczenie-Jeżeli zakres zmiany wielkości pierwszego składnika hsinę; dla całego zakresu zmiany kąta 9? leży w granicach

0 ^ h sin <p^h

to zmiana drugiego składnika (4.68) maleje do

^h 2 lciT^^h ~2kiT ^{cos2 <}P>°

-A przy minimalnych wartościach parametru k_h 6 daje dla istniejących fjjpów koparek zależność

0,083 h^h } — cos² 9?^ 0

nla niektórych typów koparek kołowych przy zmianie kąta cp od 0 do 120°, składnik (4.68) zmienia się od maksymalnej wartości (0,075 -4- 0,033) h _orZv kącie cp = 0, aż do 0 przy cp - 90°, a przy kącie cp = 50° zmniejsza £<> o połowę do (0,031 4- 0,014) h. Składnik (4.68), posiadając bardzo małe vęfertości bezwzględne, ma mały wpływ w zakresie kąta 60° < cp < 120° i dlatego można bez znaczniejszego błędu teoretyczną zależność zmiany Lubości. która ma formę dwuczłonową, zastąpić dla praktycznych zastosowań formę jednoczłonową

h_v = h sin cp m    (4.69)

Nie uwzględniamy tu wpływu parametru geometrycznego k_h.

4.6.3. Równanie funkcjonalnej zmiany szerokości 1 skiby w procesie urabiania

1 Dla określenia równania funkcji b_v — i{cp) można (rys. 4.25) napisać, że wysięg naczynia od osi Z—Z, które znajduje się w pomyślanym położeniu Kj i scharakteryzowane jest kątem cp, wynosi

R_v = A0₂ + 0₂L

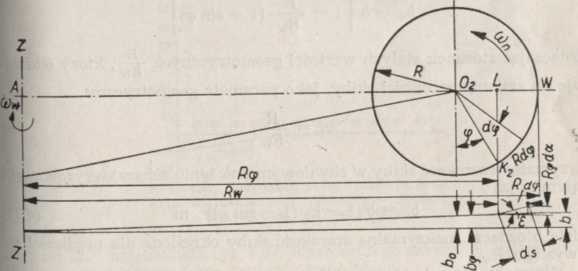
Rys. 4.25. Szerokość skiby jako funkcja położenia naczynia urabiającego [163]

Ponieważ A0₂ = Rw ~~ R, gdzie R_w oznacza wysięg naczynia od osi Z—Z, Znajdującego się na wysokości osi koła w punkcie W i 0₂L = R sin cp, dlatego wysięg R_v w położeniu K> określimy jako

R_v = R_w — R + R sin cp

Stosunek prędkości liniowych jest równy stosunkowi promieni i stąd prędkość obrotu naczynia v_K2 względem osi Z — Z w położeniu K₂, w stosunku

160