HWScan00130

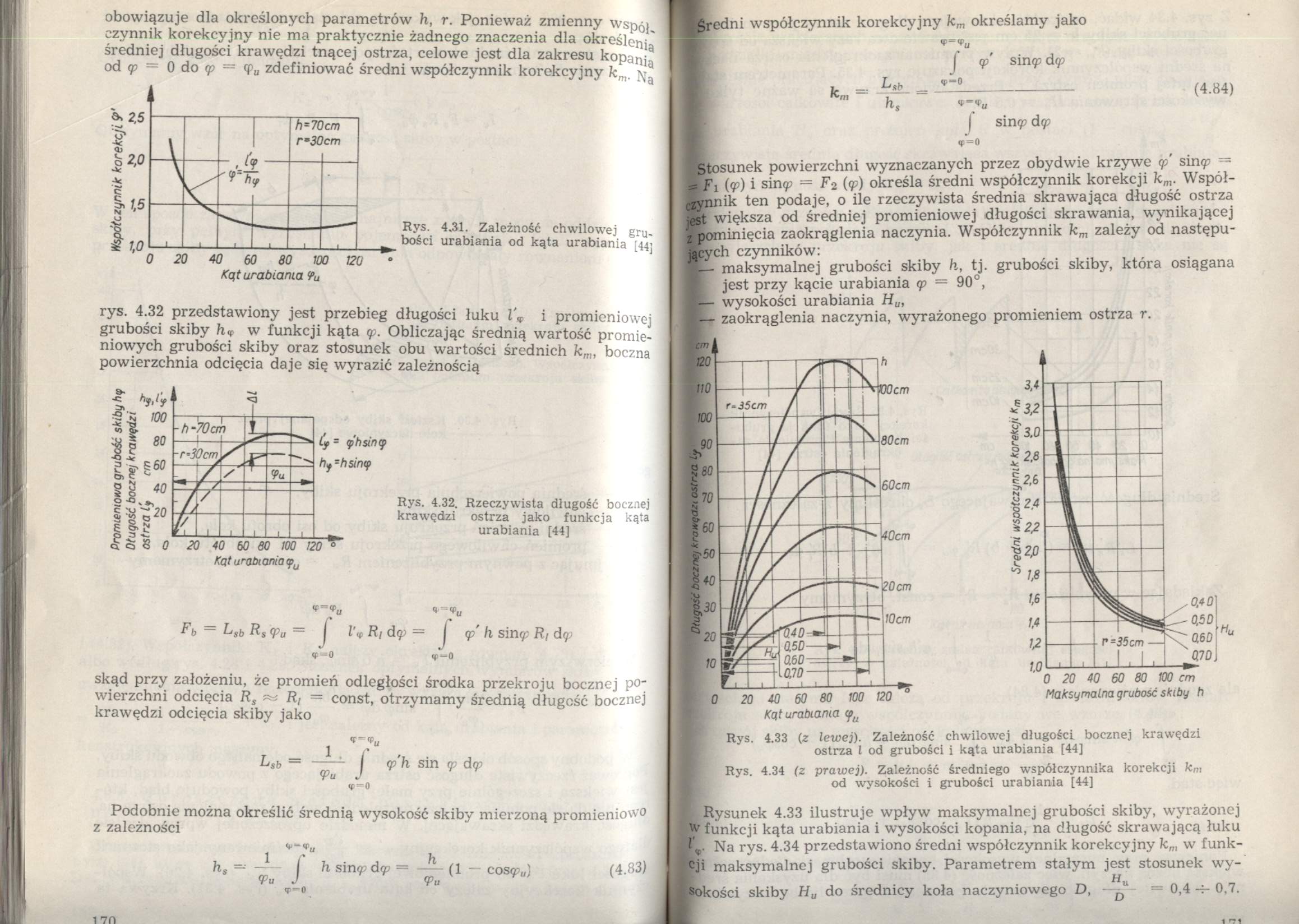
obowiązuje dla określonych parametrów h, r. Ponieważ zmienny współczynnik korekcyjny nie ma praktycznie żadnego znaczenia dla określenia średniej długości krawędzi tnącej ostrza, celowe jest dla zakresu kopania od <p = 0 do <p = qp_u zdefiniować średni współczynnik korekcyjny k_m. Na

Rys. 4.31. Zależność chwilowej grubości urabiania od kąta urabiania [44]

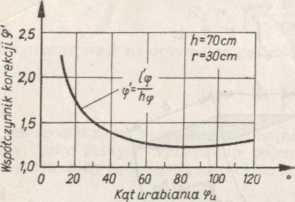
rys. 4.32 przedstawiony jest przebieg długości łuku I* i promieniowej grubości skiby h<_f w funkcji kąta tp. Obliczając średnią wartość promieniowych grubości skiby oraz stosunek obu wartości średnich k_m, boczna powierzchnia odcięcia daje się wyrazić zależnością

Cf - <p'h$ir>(p h_f ~hsin<p

60 80 Kat urabiania <p_L

Rys. 4.32. Rzeczywista długość bocznej krawędzi ostrza jako funkcja kąta urabiania [44]

«f=«p_u    « <t_u

F_b = L_sb R_s(p_u = I l\ R_tdq) = j <p' h sinę? R_t dę;

<f —0    <p“0

skąd przy założeniu, że promień odległości środka przekroju bocznej powierzchni odcięcia R_s ^ R, = const, otrzymamy średnią długość bocznej krawędzi odcięcia skiby jako

L_sb = -- I cph sin (p dq>

<Pu J

<p=0

Podobnie można określić średnią wysokość skiby mierzoną promieniowo z zależności

(4.83)

h_s —• —    | h sin<p dep = -(1 - ■ cosw_u)

<pu J    Wu

Średni współczynnik korekcyjny k_m określamy jako

k_m

Lst

h_s

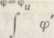
sing? d(p

ąi — O

v=«f_u

| sing? dcp

<p=0

(4.84)

Stosunek powierzchni wyznaczanych przez obydwie krzywe q> sing? — = Fi (g?) i sing? = F2 (9?) określa średni współczynnik korekcji k_m. Współczynnik ten podaje, o ile rzeczywista średnia skrawająca długość ostrza jest większa od średniej promieniowej długości skrawania, wynikającej z pominięcia zaokrąglenia naczynia. Współczynnik k_m zależy od następujących czynników:

—    maksymalnej grubości skiby h, tj. grubości skiby, która osiągana jest przy kącie urabiania q? = 90°,

—    wysokości urabiania H_u,

—    zaokrąglenia naczynia, wyrażonego promieniem ostrza r.

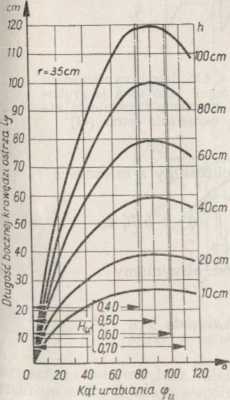
Rys. 4.33 (z lewej). Zależność chwilowej długości bocznej krawędzi ostrza l od grubości i kąta urabiania [44]

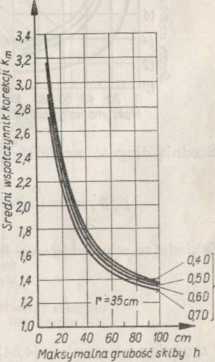
Rys. 4.34 (z prawej). Zależność średniego współczynnika korekcji k_m od wysokości i grubości urabiania [44]

Rysunek 4.33 ilustruje wpływ maksymalnej grubości skiby, wyrażonej 'y funkcji kąta urabiania i wysokości kopania, na długość skrawającą łuku *V Na rys. 4.34 przedstawiono średni współczynnik korekcyjny k_m w funkcji maksymalnej grubości skiby. Parametrem stałym jest stosunek wy-

ya sokości skiby H_u do średnicy koła naczyniowego D, _D“ = 0,4 -4- 0,7.