HWScan00204

dzanej gąsienicy wprowadza się siłę tarcia Tj między podłożem a gąsienicą, działającą w kierunku jazdy. Siła ta powstaje przy poślizgu gąsienicy przeciwnym do kierunku jazdy.

Do sił zewnętrznych należą siły tarcia wywołane przyczepnością między podłożem a gąsienicą. Siły te działają na napędzane gąsienice w kierunku jazdy Tj, a na nienapędzane gąsienice T_yJb odwrotnie, albowiem

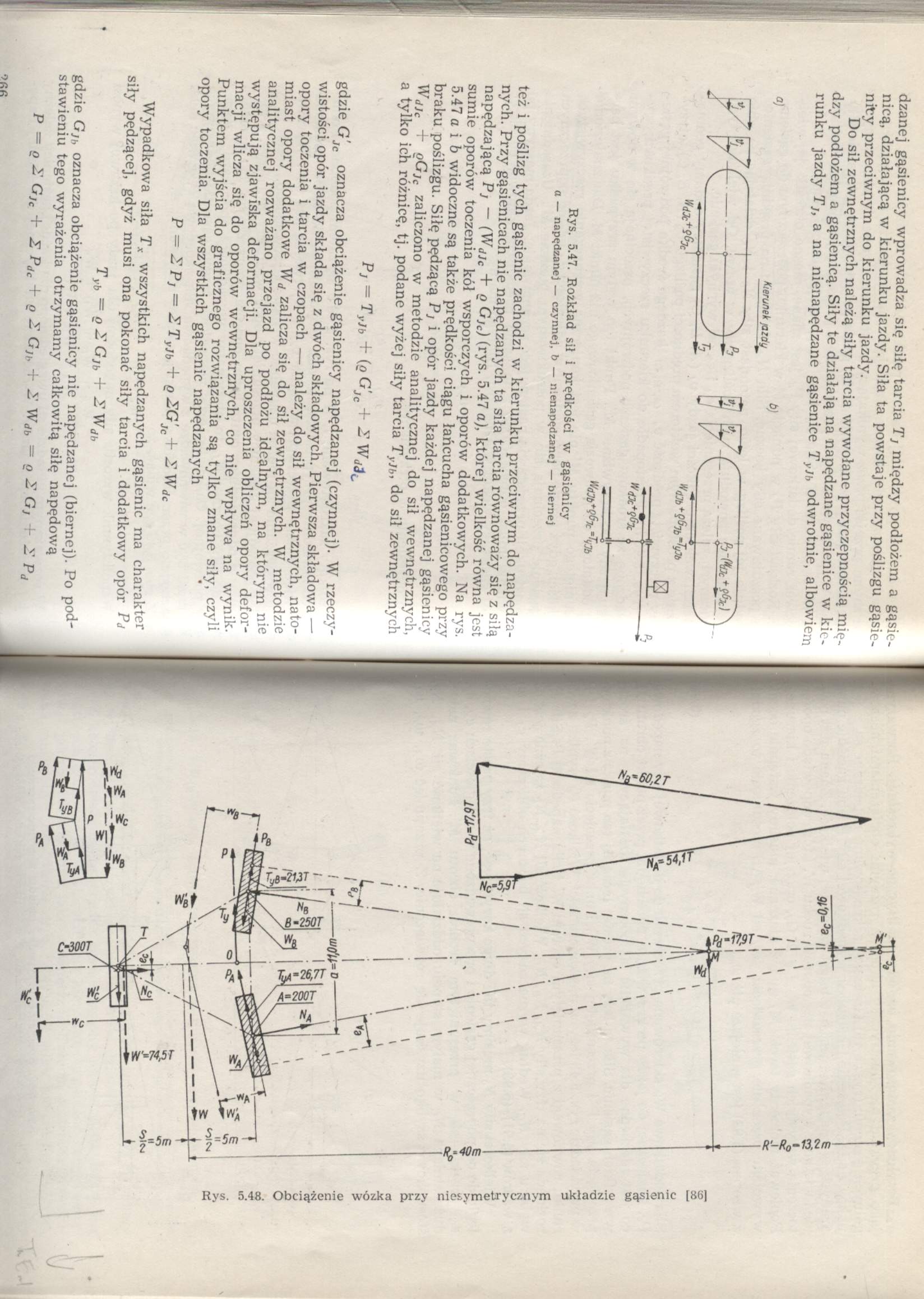
Kierunek jazdy

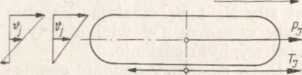
WdJc⁺9Gj_c

b)

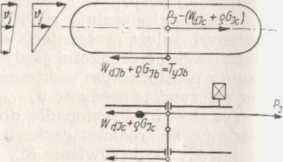
WdJb*<?Gy_c-T_vJb

Rys. 5.47. Rozkład sił i prędkości w gąsienicy a — napędzanej — czynnej, b — nienapędzanej — biernej

też i poślizg tych gąsienic zachodzi w kierunku przeciwnym do napędzanych. Przy gąsienicach nie napędzanych ta siła tarcia równoważy się z siłą napędzającą Pj — (W_dJc + o G_Jc) (rys. 5.47 a), której wielkość równa jest sumie oporów toczenia kół wsporczych i oporów dodatkowych. Na rys. 5.47 a i b widoczne są także prędkości ciągu łańcucha gąsienicowego przy braku poślizgu. Siłę pędzącą Pj i opór jazdy każdej napędzanej gąsienicy W<Uc + °Gj_c zaliczono w metodzie analitycznej do sił wewnętrznych, a tylko ich różnicę, tj. podane wyżej siły tarcia T_yJb, do sił zewnętrznych

Pj ⁼ TyJb + G? G'_Jc + Z

gdzie G'_JC oznacza obciążenie gąsienicy napędzanej (czynnej). W rzeczywistości opór jazdy składa się z dwóch składowych. Pierwsza składowa — opory toczenia i tarcia w czopach — należy do sił wewnętrznych, natomiast opory dodatkowe W_d zalicza się do sił zewnętrznych. W metodzie analitycznej rozważano przejazd po podłożu idealnym, na którym nie występują zjawiska deformacji. Dla uproszczenia obliczeń opory deformacji wlicza się do oporów wewnętrznych, co nie wpływa na wynik. Punktem wyjścia do graficznego rozwiązania są tylko znane siły, czyli opory toczenia. Dla wszystkich gąsienic napędzanych

P = ZPj = ZT_yJb + qZG'_Jc + ZW_dc

Wypadkowa siła T_x wszystkich napędzanych gąsienic ma charakter siły pędzącej, gdyż musi ona pokonać siły tarcia i dodatkowy opór P_d

T_yh = oZG_Jb + ZW_dh

gdzie Gj_h oznacza obciążenie gąsienicy nie napędzanej (biernej). Po pod stawieniu tego wyrażenia otrzymamy całkowitą siłę napędową

P = q Z G_Jc + Z P_dc + q Z G_Jb + 2- W_db — q Z Gj + Z P_d

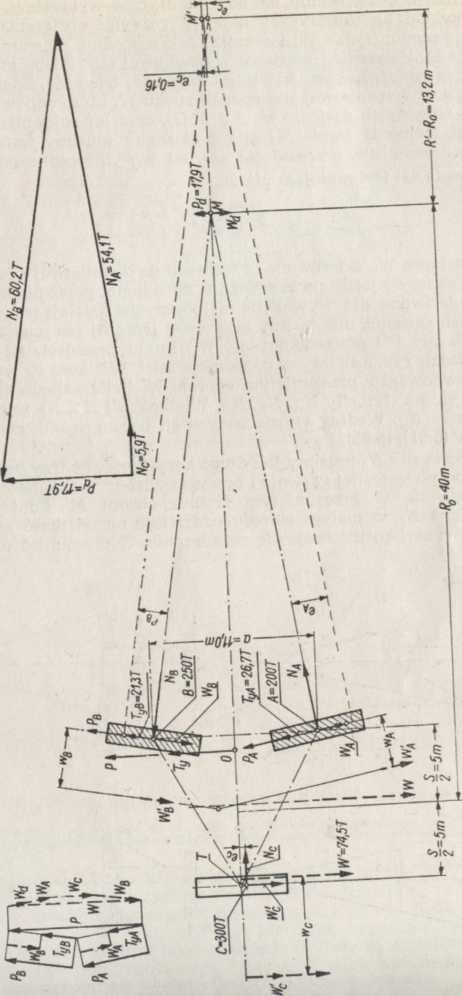
Rys. 5.48. Obciążenie wózka przy niesymetrycznym układzie gąsienic [86]