Kotwica0090

178 6. Projektowanie belek drewnianych

Jeśli w miejsce słupka wprowadzi się siłę X, powstanie zastępczy ustrój statycznie wyznaezalny, w którym

u_c = v_c    (6.29)

gdzie:

uc — ugięcie belki w punkcie C pod działaniem obciążenia zewnętrznego równomiernie rozłożonego q i siły skupionej X, mm, v_c — pionowe przesunięcie końca C słupka CD, gdyż w rzeczywistości przegub C nie przestał łączyć belki ze słupkiem, mm.

Ugięcie belki jednoprzęsłowej pod działaniem obciążenia zewnętrznego q i siły X oblicza się ze wzoru

UC =    + «c,m =    )    (6.30)

a przesunięcie punktu C (miejsca połączenia słupka z belką) ze wzoru

Vc = AIcd + &Ud    =

XIcd

NadUd

(6.31)

gdzie:

A\, Ai — odpowiednio pola powierzchni przekroju prętów 1 i 2, mm,

I_y — moment bezwładności przekroju belki, mm⁴,

Eo,mean — wartość średnia modułu sprężystości drewna wzdłuż włókien, N / mm²,

E_a    — wartość modułu sprężystości stali, N /mm².

Jeśli

Nad —

Nęp 2 sin a

X

2 sin a

(6.32)

to równanie (6.30) przybiera postać

stąd

^UClą)		XICD	XlAD
	^Ef)<mcanly	Ek),mMnA 2	2EaA\sw^2a
Y		“C.(ł)
	/3 ^lAB	lc.D .	Iad
	ĄREojneanly	Eo,meaiA2	2EqA\ sin^2 a

(6.33)

(6.34)

się w odległości

Maksymalny moment zginający w przęśle belki znajdujący —— od podpory A, wyraża się wzorem

^ACjnax — McB,ntax

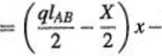
2

(6.35)

Moment zginający na podporze oblicza się ze wzoru

(6.36)

(6.37)

M»» ⁼ M_CAq) — 0,25X1ad

Siła ściskająca belkę AB

Nab = Nac = 0,5X ctg a

W belkach tego typu musi być spełniony warunek stanu granicznego nośności

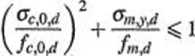
(6.38)

gdzie:

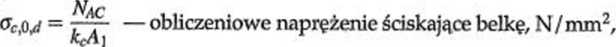
u

Om#! =    — obliczeniowe naprężenie przy zginaniu belki, N/mm²,

" V

%

y

fcfij    —obliczeniowa wytrzymałość drewna na ściskanie wzdłuż włó

kien, N/mm²,

f_m,d    — obliczeniowa wytrzymałość belki na zginanie, N/mm²,

k_c    — współczynnik wyboczeniowy wg p. 4.2.2,

W_y    — wskaźnik wytrzymałości przekroju belki, mm³.

Konstrukcje z dwoma słupkami (rys. 6.22b) przy symetrycznym ustawieniu obciążenia są ustrojami jednokrotnie statycznie niewyznaczalnymi, co oznacza, że

(6.39)

Noc* — N_Dd> — X

Konstrukcje tego typu oblicza się, przyjmując założenia wyjściowe jak w przypadku belek z jednym słupkiem.

6.5. Belki o ściankach krzyżulcowych z desek

Belkami o ściankach krzyżulcowych nazywa się konstrukcje, w których pionowe ścianki (środniki) są wykonane z krzyżujących się desek. Ze względu na kształt przekroju poprzecznego rozróżnia się belki dwuteowe (rys. 6.23e) i skrzynkowe (rys. 6.23f).

Pod względem kształtu (w widoku podłużnym) rozróżnia się belki o pasach równoległych ustawionych poziomo (rys. 6.23a) lub ukośnie (rys. 6.23b) oraz belki o pasach nierównoległych (rys. 6.23c, d).

Belki dwuteowe i skrzynkowe ze ścianką krzyżulcową łączoną na gwoździe mają najczęściej rozpiętość Ij = 9,0-f 15,Om. Zwykle przyjmuje się wysokość belek A = (1/8-i-1/1 !)<*