Kotwica0081

160 6. Projektowanie belek drewnianych

Końcowe ugięcia belki należy obliczyć ze wzoru

U fh = U_lnst (1 + k_def) < U net,f In    (6-17)

w którym:

kdef — współczynnik uwzględniający przyrost ugięcia w czasie na skutek łącznego wpływu pełzania i zmian wilgotności, wg tablicy 4.5, u_netjin — wartość graniczna ugięć wg tablicy 6.2.

■HO Przykład 6.2

Zaprojektować belkę stropową o przekroju dwuteowym łączoną na gwoździe wbijane poziomo. Rozpiętość belki w osi podpór (rozpiętość obliczeniowa) l_d = 4,80 m (rys. 6.16). Belkę należy wykonać z litego drewna sosnowego klasy C30. Ogranicza się wysokość belki do 250 mm. Obciążenie charakterystyczne na 1 m belki g = 2,00 kN/m, w tym obciążenie stałe q— 1,1 kN/m i obciążenie zmienne technologiczne średniotrwałe (działające w czasie od jednego tygodnia do sześciu miesięcy) p_k = 0,9 kN/m. Konstrukcja znajduje się w drugiej klasie użytkowania, średni współczynnik obciążenia stałego przyjęto 1,2, a obciążenia zmiennego 1,4.

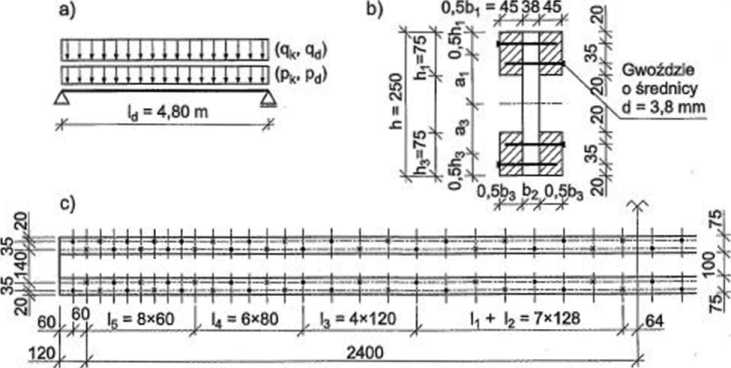
Rysunek 6.16. Belki dwuteowe łączone na gwoździe wbijane poziomo: a) schemat statyczny, b) przekrój poprzeczny, c) widok

Obciążenia obliczeniowe:

q_d = 1.1 • 1,2 = 1,32 kN/m = 1,32 N/mm

Pd = 0,9-1,4 = 1,26 kN/m = 1,26 N/mm

Największe wartości obliczeniowego momentu zginającego i siły poprzecznej:

—    od obciążenia stałego:

M_d<{q) = 0,l25q_dld = 0,125 • 1,32- 4,80² = 3,80 kN-m = 3800000 N-mm V_d<{e}) = 0,5q_dl_d = 0,5 • 1,32 -4,80 = 3,J 8 kN = 3170 N

—    od obciążenia zmiennego:

M_d>(p) = 0,125/^ = 0,125-1,26-4,80² = 3,63 kN-m = 3630000 N-mm V_dt{p) = 0,5 _Pdl_d = 0,5-1,26- 4,80 = 3,02 kN = 3020 N

Wartości charakterystyczne wytrzymałości drewna litego klasy C30 (tabl. 3.2):

—    na zginanie /„,^ = 30 N/mm²,

—    na ścinanie /„* = 3,0 N/mm².

średni charakterystyczny współczynnik sprężystości wzdłuż włókien (tabl. 3.2) £o,/»dwr = 12 kN/mnr² = 12000 N/mm²

Wartości obliczeniowe wytrzymałości drewna litego klasy C30 ustalono przyjmując współczynnik modyfikacyjny k_mod dla obciążeń o najkrótszym czasie trwania. W rozpatrywanym przypadku (obciążenie zmienne technologiczne działające przez okres od jednego tygodnia do sześciu miesięcy) w drugiej klasie użytkowania przyjęto = 0,80 (tabl. 3.10). Odpowiednie wytrzymałości obliczeniowe drewna sosnowego klasy C30:

fm/ł ~

fm,kKnod

30-0,80

1,3

= 18,46 N/mm²

1,85 N/mm²

f fyjjkmod _ 3,0-0,80 7*    1,3

Potrzebny wskaźnik wytrzymałości i moment bezwładności przekroju belki z uwagi na zginanie:

...    Muri+M* W 3800000 + 3630000 .........,

W_y =---=-——-= 402500 mnr

fm4    18,46

I_y = \vĄ =402500— = 50312500 mm⁴

Obliczenie momentu bezwładności przekroju ze względu na ugięcie Zakłada się, że belki będą elementem dachu, zatem graniczne ugięcie belki

^unel,fin —

Jd_

200

4800

200

= 24,0 mm