Kotwica0086

170 6. Projektowanie belek drewnianych

llilO Przykład 6.3

Zaprojektować belkę stropową o rozpiętości w świetle podpór (ścian nośnych) / = 8,0 m (rys. 6.18). Przyjęto belkę złożoną z dwóch elementów skonanych z drewna sosnowego klasy C30 o wilgotności nie przekraczającej 12%. Klocki z drewna dębowego klasy D50. Śruby ze stali StOS (wg PN-90/B-03200) o f_d~ 165 N/mm². Konstrukcja znajduje się w pierwszej klasie użytkowania (wg PN-B-03150:2000).

Obciążenie charakterystyczne stałe równomiernie rozłożone (wraz z ciężarem belki) q_k = 2,33 kN/m, obciążenie użytkowe p_k = 3,00 kN/m. Przewiduje się, że obciążenie to

a)

Hllli] lilii lignit) in u; ji nu mrnKftc,Pd) Aa-&^B

„ Id = 8.40 m “

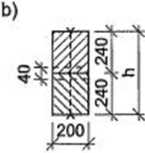
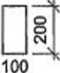
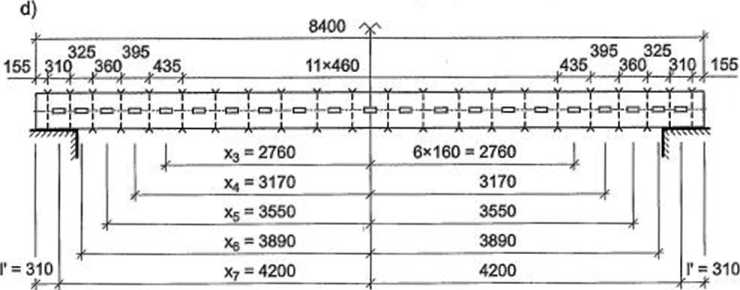
Rysunek 6.18. Belka drewniana złożona z dwóch elementów łączonych na klocki: a) schemat statyczny, b) przekrój belki, c) przekrój i rzut kołka, d) widok belki

będzie oddziaływać przez okres od 1 tygodnia do 6 miesięcy (obciążenie średniotrwałe). średni współczynnik obciążenia stałego przyjęto 1,2, a obciążenia zmiennego 1,4. Obciążenia obliczeniowe:

g_d = 2,33 1,2 = 2,80 kN/m = 2,80 N/mm p_d = 3,00 • 1,4 = 4,20 kN/m = 4,20 N/mm Teoretyczna rozpiętość belki

l_d = 1,05/ = 1,05 • 8,0 = 8,40 m = 8400 mm

Największy obliczeniowy moment zginający i siła poprzeczna:

— od obciążenia stałego:

M_d(q) = 0,125p_dl_d = 0,125 • 2,8 • 8400² = 24696000 N mm V_d>{q) = 0,5p_dl_d = 0,5 • 2,8 • 8400 = 11760 N

6.3. Belki o przekroju złożonym łączone na klocki łub pierścienie

171

— od obciążenia zmiennego:

M_dt{p) = 0,125p_dl] = 0,125-4,2 • 8400² = 37044000 N-mm

^vd,(_P) = 0,5 pjlj = 0,5 • 4,2 • 8400 = 17640 N

Wartości charakterystyczne wytrzymałości drewna sosnowego litego klasy C30 (tabL 3.2):

—    na zginanie = 30 N/mm²,

—    na ścinanie f.j. = 3,0 N/mm².

Wartości charakterystyczne wytrzymałości na ścinanie drewna dębowego litego klasy D50 (tabl. 3.3)

— 4,6 N / mm²

Średni charakterystyczny współczynnik sprężystości wzdłuż włókien drewna sosnowego klasy C30

Eosnean = 12 kN/mm² (GPa) = 12000 N/mm²

Współczynnik modyfikacyjny przyjęto dla obciążenia o najkrótszym czasie trwania, w tym przypadku średniotrwałego, przy którym k_m>d = 0,8 (tabl. 3.10).

Wytrzymałości obliczeniowe w przypadku drewna sosnowego:

_r fm,kkmod 30-0,80 _to ,_rNT/ 2 fm4 = —~-= —rT~ = ¹⁸>⁴⁶ N/nurr

JM    *

f,₄ =    = 1,85 N/mm²

/    =    = 5^ ₌ 3,51 N/mm²

Tm    1,3

Wytrzymałość obliczeniowa w przypadku drewna dębowego

= 2,83 N/mm²

_e _ fvjcknwd _ 4,6-0,80

^fv4~ m--

Potrzebny wskaźnik wytrzymałości przy założeniu pełnego wykorzystania przekroju

= 4777900 mm³

M_dAg)+M_{d {p)} _ 24 960000-r 37 044 000 n_wfm4 ~    0,7-18,46

Przyjęto dwa elementy o wymiarach przekroju 200x240 mm (rys. 6.18).

Zastępczy wskaźnik wytrzymałości i moment bezwładności przekroju przy założonych współczynnikach poprawkowych (n_w = 0,7 i m — 0,56) dla belek złożonych z dwóch elementów:

^WW =    ^ = 0,7 • ^2Q0'^48Q1 = ₅ 376000 mm³

1„f = «,~ = 0,56 • ²⁰⁰ ^⁸⁽⁾³- = 1032192000 mm⁴ Naprężenia normalne w najbardziej wytężonym przekroju

A0i) + A^.(p)    24960000 + 37044000

Wyjf ~    ~ 5376000

= 11,48 N/mm² <    = 18,46 N/mm²