Kotwica0095

188 6. Projektowanie belek drewnianych

a)    b)

mJlllłJHTllllJliri(qk.qd) Szczegół A Szczegół B Szczegół C

c)

d)

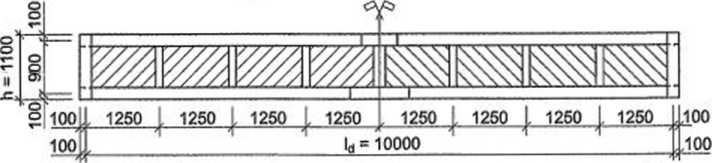
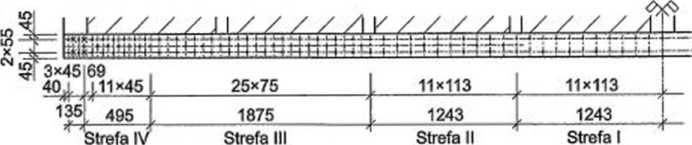
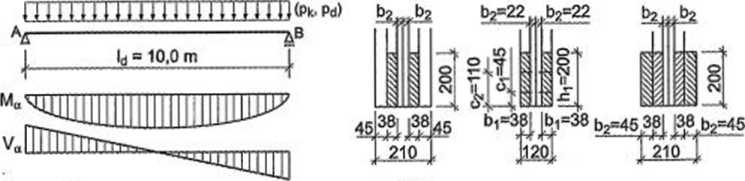
Rysunek 6J0. Belka dwuteowa ze ścianką krzyżulcową łączoną na gwoździe: a) schemat statyczny, b) szczegóły połączenia pasów ze środnikiem i słupkami, c) widok belki, d) rozmieszczenie gwoździ w pasach górnym i dolnym, e) widok strefy przypodporowej, f) widok strefy środkowej i połączenia pasów

Największe wartości obliczeniowego momentu zginającego i siły poprzecznej:

Mmax = 0,125{q_d + p<*)/² = 0,125 • (5,18+ 3,90) • 10,0² = 113,5 kN-m » 113500000 N-mm

Vmox = 0Ć(<ld+Pd)l = 0,5 • (5,18 + 3,90)-10,0 = 45,4 kN = 45400 N

Wartości charakterystyczne wytrzymałości zastosowanego drewna jodłowego (tabl. 3.2):

—    na zginanie f_mJ( — 0,8 ■ 30,0 = 24,0 N/mm²,

—    na ścinanie /_vjt - 0,8 • 3,0 = 2,4 N/mm²,

—    na ściskanie równoległe do włókien f_c0ik = 0,8 • 23,0 = 17,4 N/mm².

Średni charakterystyczny współczynnik sprężystości wzdłuż włókien dla drewna jodłowego klasy C30 (tabl. 3.2)

E_0tmean = 0,8 • 12,0 = 9,6 kN/mm² = 9600 N/mm²

5-proc. kwantyl modułu sprężystości wzdłuż włókien

Eo,05 ~ 0,8 • 8,0 = 6,4 kN/mm² = 6400 N/mm²

Współczynnik modyfikacyjny dotyczący klas obciążenia przyjęto dla obciążeń o najkrótszym czasie trwania. W niniejszym przykładzie jest to obciążenie średniotrwałe, zatem kmod = 0,80 (tabl. 3.10).

Wytrzymałości obliczeniowe:

= 14,77 N/mm²

_t _ fmjik_inMi 24,0-0,80

^fm*—n,---

ę    fv,k^-mod    2,4 • 0,80

Jv,d

= 1,48 N / mm²

Wysokość belki

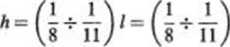
•10000= 1250 + 910 mm

Przyjęto belkę wysokości h = 1100 mm. Pasy i ścianki z desek o wymiarach przekroju odpowiednio 38x200 mm i 22x 160 mm.

Sprawdzenie warunku stanu granicznego nośności

Przekrój sprawdza się przyjmując moment bezwładności l_ntUo po potrąceniu otworów na sworznie, których średnicę założono wstępnie d = 14 mm. Zatem

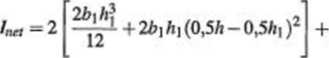
(0,5 1100- 110)²

= 5302620000 mm⁴