MG!31

Ody fntlhd wtoftdct i t y JM normalny lub zbliżony do normalnego. ID ńtnkcję liglNjl traktuje alf Jdo AmIk)| liniową o równaniu

(1.28)

y • aa ♦ P

funt metry ■ i p liniowej funkcji ngniji okrc.Ha sią ta pomocą metody najmniejszych kwadratów. To tnąc ty Żąda się, aby dla danych t próby n waitofei i₍, y₍ funkcja • określona wtórem (1.29), osiągnęła lujmnujiii wartość

(1.29)

• • £ (y, •• ■«, - P)²-

Prowadzi to, po zastosowaniu warunku koniecznego i dostatecznego na istnienie minimum ftmkcji dwu zmiennych, do układu dwóch równań linio* wych. którego rozwiązanie duje szukane oszacowanie parametrów a i p. Parametr a nosi nazwą współczynnika regresji y względem x i wyraża średnią zmianą wartości y, w przypadku gdy x zmieniła wartość o jedną jednostką. Korzystąjąc z założenia o normalności rozkładu, można zbudować przedział ufności dla współczynnika regresji oraz krzywe ufności dla prostej regresji. Przedział ufności dla współczynnika regresji a wyznacza sią według wzoru

gdzie współczynnik regresji a, uzyskany na podstawie metody najmniejszych kwadratów, równa sią

m

E to - **)(?! - Ł)    Ew” ^x*y*

a ■

/>!

(1-31)

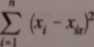
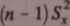
a odchylenie przeciętne dla prostej regresji S_r oblicza się z zależności

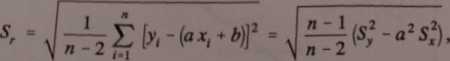
(1.32)

gdzie:

^{b =} y*~^axfr*

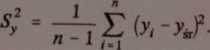
WmaM mmmmi Imowrj L    afciymji wę « Mky U <fli

mtośamęo prawdopodohiadrtwa.

1.9. Btfdy wyników złożonych. Httodi różniczki zupełno)

W praktyce laboratoryjnej Wdo caęM iyaacMl «ą widet, będące funkcja jednej lub kilku iMmydi taiokt ftmty pnypM tego rodzaju zachodzi. gdy chce st< m przykład lyMrtjf pak pbintM kola Mne jego średnice Pole powierzchni kok jM funkcją jednej BHMMJ (kkcyl wyznaczonej doświadczalnie

Z bardziej złożonym przypadkiem można mieć do czynienia przy wytmamm np. modułu Younga a pomocą tnuoMw elcktiooporomej Wwl niri— Morzonymi są: siła obciążająca próbkę, względne wydhizmic próbki oraz jej wymiary. Obliczony ostatecznie moduł Younga jen funkcją kilku zmiennych ustalonych na podstawie pomiarów. Powstaje pytanie, jak obliczać w takich przypadkach ostateczny błąd wyniku na podstawie błędów poszczególnych mierzonych wielkości, jak znaleźć udział poszczególnych błędów w blęd/ie wyniku kotkowego? Zagadnienie to będzie rozwiązane za pomocą rachunku różnic iko we go.

Rozpatruje się najpierw prosty przypadek, w którym szukany wynik zależy tylko od jednej zmiennej wielkości, obarczonej błędem pomiarowym Az. Niech a będzie szukanym wynikiem, jako określona funkcja /U) wielkości z. Jeżeli Az jest średnim bezwzględnym błędem wielkości z, przy czym Az<x, to błąd szukanej wielkości a jest równy iAa. Można więc napisać

(1.33)

a ± Aa = /(z ± Az).

Po rozłożeniu prawej strony na szereg Taylora otrzymuje się

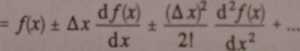
a i Aa

Zaniedbując w rozwinięciu człony, w których Az występuje w stopniu wyższym niż pierwszy, otrzymuje się

dz

a± Aa = /{x)±4® Az.

Jeśli uwzględni się, że a = /(z), ostatecznie uzyska się

(134)

|Aa| = Az. dz

Błąd bezwzględny funkcji równa się iloczynowi bezwzględnego błędu mierzonej wielkości i pochodnej tej funkcji.

23