MG!62

Układy pomiarowe do pomiarów statycznych i dynamicznych są zasilane z reguły prądem zmiennym. Zasilaczem jest wtedy generator zmiennoprądowy o częstości nośnej w zakresie od 1 kHz (pomiary statyczne) do 8 kHz (pomiary dynamiczne). Zaletą układów zmiennoprądowych są: możliwość używania stosunkowo prostych i tanich wzmacniaczy sygnału oraz niewrażliwość układu na zmiany temperatury otoczenia. Główną wadą jest natomiast ograniczenie częstości mierzonych przebiegów do około 20% częstości nośnej zasilacza.

3.2.4. Teoria płaskiego stanu odkształcenia

Dotychczas rozpatrywane były jednoznaczne przypadki odkształcenia, towarzyszące jednoosiowemu rozciąganiu, prostemu zginaniu czy też skręcaniu. W ogólnym przypadku obciążenia zazwyczaj nie są znane kierunki i wartości naprężeń głównych określających stan naprężenia w rozpatrywanym punkcie. Należy więc doświadczalnie wyznaczyć te wielkości. Za pomocą tensometrów określa się każdorazowo odkształcenie wzdłuż linii ich naklejenia. Konieczne staje się przeprowadzenie analizy stanu odkształcenia, aby na podstawie zmierzonych wielkości odkształceń obliczyć wartości naprężeń głównych.

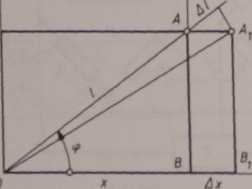
Wydłużenie względne e_ę, mierzone w kierunku osi l (nachylonej pod kątem <p do osi układu), można w prosty sposób uzależnić od wydłużenia e , mierzonego w kierunku osi x (rys. 3.14). Odkształcenie prostokąta ABOD

D

t

x

Rys. 3.14

spowoduje wydłużenie odcinka OA o długości l o wartość A/. Jak widać na rys. 3.14, między tymi wielkościami a ich rzutami na oś x zachodzą zależności

(3-13)

czyli

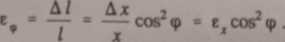
(3.14)

84

Przeprowadzając podobne rozumowanie dla przemieszczenia końca A odcinka I w kierunku osi y do punktu A₂ uzyskuje się

t_ę | e_ysin²<p.    (3-15)

W przypadku postaciowego odkształcenia powierzchni, wynikającego i działania naprężeń tnących, prostokąt ABOD przekształci się w równoległo* bok ABOD_x (rys. 3.15). Przyrost długości przekątnej OA zależy od kąta q> oraz kąta odkształcenia postaciowego y . Z geometrii wynika

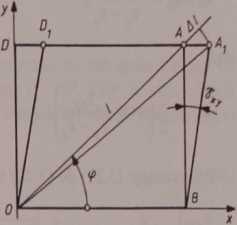
AA_{= AB tgy_xy.    (3.16)

Uzależniając AB i AA_X od długości przekątnej l jej przyrostu i kąta <p

^AB * ¹™^V-    (3.17)

A l = >4/1, cos<p,

otrzymuje się po przekształceniu A/ .

e„ = —— = tgy sm<p costp.

* j    ^{T r}    Rys. 3.15

Ponieważ rozważania ograniczają się do małych odkształceń, zakłada się tgT„ “ V ^skąd

e = y_xysin<p costp.    (3.18)

Jeżeli omówione wyżej przypadki odkształcenia powierzchni wystąpią równocześnie, wtedy wydłużenie względne e_f będzie sumą wydłużeń opisanych związkami (3.14), (3.15) i (3.18), co można przedstawić następująco

e_f = e_xcos²tp + e_y sin² cp + sin cp cos<p.    (3.19)

Wprowadzając odpowiednie funkcje podwojonego kąta <p otrzymuje się

«, * \ («,⁺|(«. -    ⁺1    S

W zależności (3.20), określającej związek między wydłużeniem względnym e a składowymi odkształcenia w obranym układzie współrzędnych prostokątnych x, y, niewiadomymi są wydłużenia względne mierzone w kierunku osi układu e_x, e i kąt odkształcenia postaciowego y . Aby wyznaczyć te trzy wartości, wystarczy zmierzyć odkształcenia w trzech dowolnych kierunkach i rozwiązać układ równań

^ef,■ \ (^e*⁺ e/)⁺\ (^e* - ^c,)^cos2(Pł ♦    ²9,,    ^(3<21)

85