3582445227

4.    Zbuduj kąt /?; /?e(90°, 180°) mając dane:

a) cos/? = —0,3;    c) tg/? = —5;

b) sin/? = 0,7;    d) ctg/? = 3.

5.    Zbuduj kąt (p; <pe(180°, 270°) mając dane:

3    .    1 ,

a) ctg (p = 6; b) cos <p = —    c) sin <p = — -.

6.    Zbuduj kąt y; ye(270°, 360°) mając dane:

„ a) tgy = —0,1;    b) siny = — 0,8;    ..._t . c) cosy = 0,9.

7.    W której ćwiartce leży końcowe ramię kąta a, jeśli:

a)    | sin a | = —sina;

b)    | cos a | = cos a;

c)    |sin(—a)| = —sina;

d)    I tg a | = tg a;

e)    |ctg(—a) | = —ctga.

IY.3. WŁASNOŚCI FUNKCJI TRYGONOMETRYCZNYCH

A.    Okresowość funkcji trygonometrycznych sin (k • 360° + a) = sin a

cos (k • 360° + a) = cos a . i keC tg (k-180° + a) = tg a

ctg(fc-180° + a) = ctg a    .

B.    Związki między funkcjami trygonometrycznymi tego samego kąta: sin² a + cos² a =1;

sin a    ,    n    .    ,    „

-= tg a, gdy a ^ - + kit. i keC    -

cos a    2    _s.i

cos a    ,    ,    .    ,    _ '

—— =    tg a,    gdy oi    ^ kn    i    keC

sina    •    '......

tga-ctga=l,    gdy a    ^k-    i    keC.

C.    Parzystość i nieparzystość funkcji trygonometrycznych

sin (—a) = —sina    ;^;v

cos(—a) = cosa    -

tg (—a) = —tg a ctg(-a) =-ctga

D.    Wzory redukcyjne:

Umiejętność stosowania wzorów redukcyjnych pozwala na sprowadzenie kąta o dowolnej mierze do kąta ostrego.

(p	90° - a (i-)	90° +a (!*■)	180° - a (n-a)	180° + a (* + *)	270° - a (H)	270° + a (r^+‘)	360° — a (2 x - a)
sin ę	cos a	cos a	sina	—sina	—cos a	—cos a	—sina
COS (p	sina	—sina	—cos a	—cos a	—sina	sina '	cos a
tg (p	ctg a	-ctg a	-tga	tga	ctg a	-ctg a	-tga
ctg q>	tg a	—tga	-ctg a	ctg a	tga	-tga	-ctg a

1.    Oblicz bez użycia tablic matematycznych:

a)    sin 1200° + cos (-1080°);    d)    3 cos (-300°) sin 45° • tg 135°;

b)    4 sin 120° • tg 300°;    e)    2 sin² 225° - ctg 330° tg 405°;

c)    2 sin 120° - tg 240°;    f)    10 ctg 315° sin (-150°) cos 225°.

2.    Oblicz bez użycia tablic matematycznych:

sin² 120°-cos (—180°) ^a) tg (-135°) ctg 405° ’

9 sin 150° - 4 cos 240° + 12 sin 600°

•    ‘ 3 sin (—45°) — 2 cos (-420°)    ’

c) tg 10° tg 20° tg 30° tg 40° tg 50° tg 60° tg 70° tg 80°; sin(« — 180°) cos(810° + «) — cos(« — 90°) sin(720° — «) sin (360° + a) sin (540° — a)

3.    Uprościć wyrażenie

sin (a — 180°) cos (450° — a) sin (540° + a) cos (—270° + a) ’

cos(180° — a) sin(—a) ctg(—a — 90°)    •

' tg (540° + a) cos (-270° + a) ’ c) sin(—328°) sin 598° tg 572° + cos 1022° cos(-148°) ctg 32°;

’d) cos(—7,9tt) tg(—1,1 n) — sin 5,6n ctg 4,4n;

e) sin5,27r-sin(— 3,7;r)-tg(— 3,27t) — cos(— 2,7ti)-cos(— 11,87r)• ctg(— 0,2tt).

4. Oblicz wartości funkcji: „ _ _% 2sinacosa a) m =

sin 2 a b) /(a) = tg2a -

O) m -

dla a = -300°;

sin 2 a 4 cos a — 2 2 (cos² a — sin² a)

sin 2 a

dla

dla

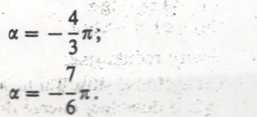
66