7409411823

AADC    ADBC

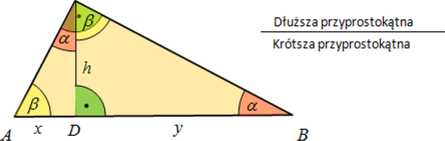
Trójkąt ABC ma kąty: a . fi. 9 0°.

Trójkąt ADC ma dwa kąty znane: <ADC = 90° oraz <DAC = /S Zatem trzeci kąt <ACD = a

Trójkąt BCD ma dwa kąty znane: <BDC = 90° oraz <DBC = a Zatem trzeci kąt <BCD = fi

Zauważamy, że A<iDC ~ ADBC na podstawie cechy podobieństwa trójkątów kąt-kąt.