3093695800

F. T r 9. i k ą t.. r ó w no r ą mi e.nny

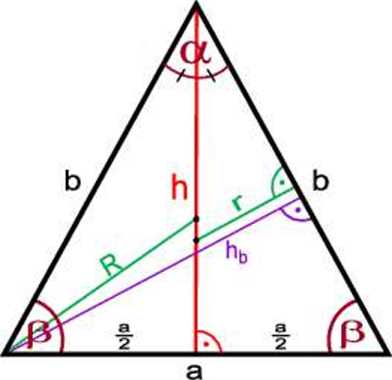
Trójkąt równoramienny - ma dwa boki (ramiona) i dwa kąty (przy podstawie) równe. Wysokość (h) poprowadzona z podstawy (a): jest dwusieczną kąta (a) leżącego naprzeciwko podstawy; jest symetralną podstawy (dzieli podstawę na dwie równe części): dzieli trójkąt równoramienny na dwa przystające trójkąty prostokątne.

Pole trójkąta:

•b-h_b

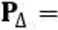
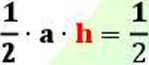
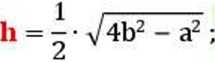
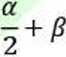
90°

gdzie:

a - podstawa trójkąta; b - ramię trójkąta h - wysokość trójkąta poprowadzona do podstawy a hi, - wysokość trójkąta poprowadzona do ramienia b r - promień okręgu wpisanego w trójkąt R - promień okręgu opisanego na trójkącie

G. Xf.óik31..r ó w n o b o cz ny

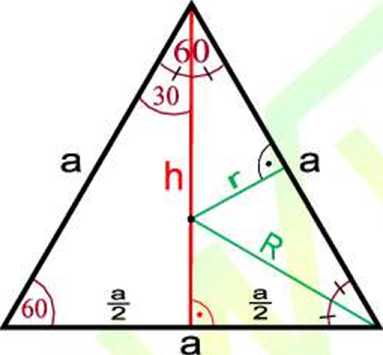
Trójkąt równoboczny - ma wszystkie boki (a) i kąty (a = p = y = 60°) równe. Wysokości są jednocześnie symetralnymi boków, dwusiecznymi kątów oraz środkowymi trójkąta równobocznego.

a • li a² ■ v3

^Pa=~⁼    4

1 , a • v 3 r = -h =——;

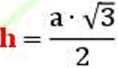
= R+ r

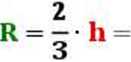
a -V3 3

gdzie:

Pa - pole trójkąta

a - bok trójkąta; h - wysokość trójkąta r - promień okręgu wpisanego w trójkąt R - promień okręgu opisanego na trójkącie

H. Rozwi.iązywąnje..tróikątów_>-

Wielkości dane	A	Sposoby obliczania wielkości szukanych / uwagi
Bok i kąt ostry	prostokątny	Drugi kąt ostry = 90° minus kąt dany. Szukane boki - z funkcji trygonometrycznych w A prostokątnym. Rozwiązanie istnieje zawsze.
Dwa boki		Trzeci bok - z twierdzenia Pitagorasa. Kąty - z funkcji trygonometrycznych w A prostokątnym. Rozwiązanie istnieje o ile suma długości dwóch boków jest wiesza od długości trzeciego boku.
Trzy boki	dowolny	Kąty - ze wzorów co sinusów. Rozwiązanie istnieje o ile suma długości dwóch boków jest większa od długości trzeciego boku.
Dwa boki i kąt między nimi		Trzeci bok - ze wzorów c osi nu sów. Kąty - ze wzorów sinusów lub c osi nu sów. Rozwiązanie istnieje zawsze.
Dwa kąty i bok między nimi		Trzeci kąt - z sumy kątów w A (180°). Boki - z wzoru sinusów. Rozwiązanie istnieje., gdy suma danych kątów jest mniejsza od 180°.
Dwa boki i kąt leżący naprzeciw jednego z nich		Trzeci bok- z wzoru sinusów. Drugi kąt - z wzoru sinusów. Trzeci kąt - z sumy kątów w A (180°). Rozwiązanie istnieje o ile suma długości dwóch boków jest wiesza od długości trzeciego boku.

© Copyright by Ewa Kędzi orczyk    -301 -    www.matematyka.sosnowiec.pl