Untitled Scanned 26 (8)

PLANIMETRIA 29

2.63    R Ramię trójkąta równoramiennego ma długość h. a kąt przy podstawie ma miarę a. Wyznacz długość promienia

a)    okręgu opisanego na trójkącie;

b)    okręgu wpisanego w trójkąt.

2.64    R Jeden z boków trójkąta ma długość a. zaś kąty trójkąta przyległe do tego boku mają miary a i //.

a)    Znajdź promień okręgu opisanego na tym trójkącie.

b)    Wyznacz długości pozostałych boków trójkąta.

c)    Znajdź promień okręgu wpisanego w ten trójkąt.

2.65    R Długości dwóch boków trójkąta są równe I i 4, a miara kąta zawartego między nimi wynosi 00°.

a)    Oblicz promień okręgu opisanego na tym trójkącie.

b)    Oblicz promień okręgu wpisanego w ten trójkąt.

%

2.66    R Boki trójkąta mają długości 4, K i 10.

a)    Oblicz kosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.

b)    Oblicz długość środkowej poprowadzonej do najdłuższego boku.

2.67    R Długości boków trójkąta są w stosunku 2:3:4. Oblicz kosinus największego kąta tego trójkąta.

2.68    R Na boku LM trójkąta równobocznego KLM obrano taki punkt zł. że |/łjW|:|/lL|=4: I.

a)    Oblicz stosunek pól trójkątów KIA i KAM.

b)    Oblicz stosunek promieni okręgów opisanych na trójkątach KIA i KAM.

c)    Wyznacz sinus kąta LKA.

ZADANIA MATURALNE

TRÓJKĄTY

136. Kąt RAC trójkąta ABC ma miarę 13°, a kąt ACB miarę 11*J°. Wysokość CD dzieli bok AR na dwa odcinki, 7. których krótszy ma długość 25 cm. Oblicz długość boku AC.

137. Dwa kąty trójkąta mają miary 30° i 50°. Oblicz miarę kąta, jaki tworzy dwusieczna trzeciego kąta z wysokością poprowadzoną z wierzchołka tego kąta.

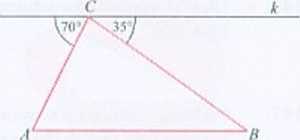
138. Oblicz miary kątów trójkąta ABC (patrz rysunek obok) wiedząc, że AR || k.

139. n W ostrokątnym trójkącie równoramiennym ramię ma długość 6I. a wysokość poprowadzona do ramienia ma długość 11.

a)    Oblicz pole tego trójkąta.

b)    Oblicz długość podstawy tego trójkąta.