2210689704

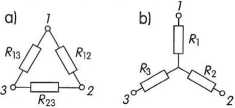
Rys. 17. Układy połączeń rezystorów między trzema punktami węzłowymi: a) w trójkąt; b) w gwiazdę [2]

Korzyści wynikające z przekształcenia układu, na przykład trójkąta w gwiazdę, stają się oczywiste, jeżeli rozpatrzymy obwód rozgałęziony przedstawiony na rysunku 30 a. W obwodzie tym nie ma gałęzi, w których rezystory byłyby połączone szeregowo oraz nie ma gałęzi połączonych równolegle. Między węzłami 1, 2, 3 rezystory (gałęzie) są połączone w trójkąt. Jeżeli układ ten (zawarty między węzłami 1, 2 i 3) zamienimy układem połączeń w gwiazdę, to schemat elektryczny obwodu uzyska postać taką, jak na rys. 30 b. W obwodzie tym można wykonać proste przekształcenia szeregowo i równolegle połączonych elementów. W konsekwencji otrzymamy prosty obwód nierozgałęziony zawierający jedno źródło napięcia i jeden element odbiorczy (rys. 30 c.).

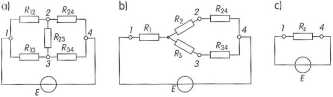
Rys. 18. Sposób przekształcania obwodu zawierającego rezystory' połączone w trójkąt: a) obwód pierwotny: b) obwód po przekształceniu połączeń z trójkąta w gwiazdę; c) obwód zastępczy' [2]

Aby obliczyć rezystancję zastępczą R_z, konieczna jest znajomość zależności rezystancji Ri, R2 i R3 od rezystancji R12, R13 i R23. Zależności te wprowadza się przy założeniu, że dwa fragmenty obwodu są równoważne, jeżeli ich rezystancje wypadkowe, mierzone między dwoma dowolnymi parami odpowiadających sobie punktów, są jednakowe. Mają one postacie:

^R12^R13

^RI2 + ^R13 ^{+ R}23 ^Rl 2 ^R23

R|2 + R|3 + R93

Ri =

R₂ =

R₃ =

^Rl 3 ^R23

Rj2 + R|3 + R23

Można również przekształcić układ połączony w gwiazdę w równoważny mu układ połączony w trójkąt. Rezystancję poszczególnych gałęzi układu połączeń w trójkąt oblicza się z następujących zależności:

„    „ R, R,

Rl2 = R| + R2 + -,

R,