4544138939

Jerzy Wasiluk, Aleksander Ostanin

	A	B	c	D	E ■■	F
1
2	X1	X2	X3	Wyrazy wolne	Wynik
3	1	2	3	14	x1 = 1
4	4	3	-1	7	x2 =	2
5	1	-1	1	2	x3 =	3

Rys. 9. Tablica z rozwiązaniem pobranym z Matlaba

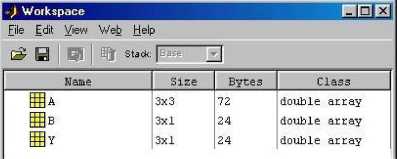
Rys. 10. Okno dialogowe "Workspace"do wyboru macierzy do obejrzenia w Matlabie

3.2 Wymiana informacji tekstowej

1. Utworzyć macierz Miesiąc. Utworzymy w Excelu tablicę z danymi

Tabela 2. Tablica z danymi tekstowymi

	A	B	C
1	Styczeń	Luty	Marzec
2	Kwiecień	Maj	Czerwiec
3	Lipiec	Sierpień	Wrzesień
4	Październik	Listopad	Grudzień

2. Zaznaczyć na tablicy obszar A1:C4 i wybrać przycisk putmatrix. Spowoduje to otwarcie okna dialogowego, pokazanego na rysunku 11, w którym należy wpisać nazwę dla tworzonej w Matlabie macierzy Miesiąc. W wyniku wykonania funkcji MLPutMatrix w obszarze roboczym programu MATLAB pojawiła się macierz o

166