Funkcja malejaca
FUNKCJA MALEJĄCA
A
x>J,
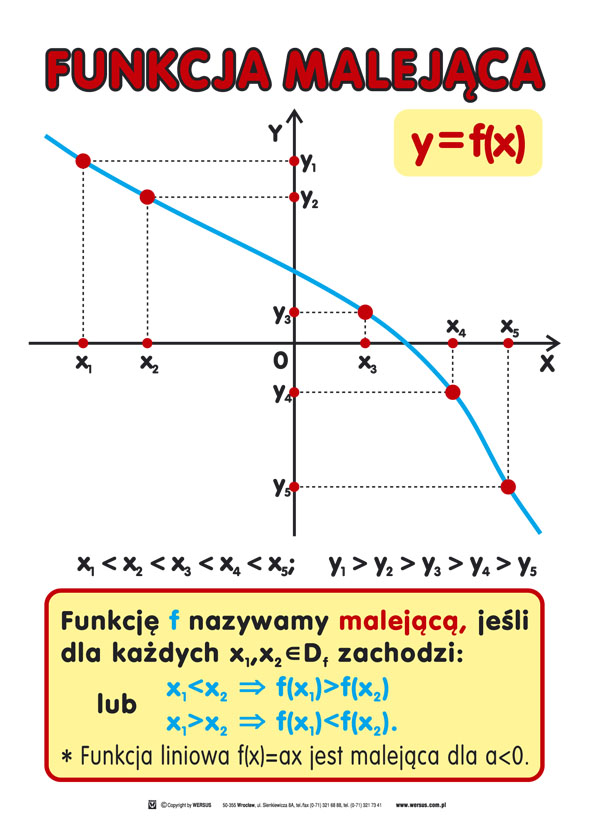
x1<x2<x3<x4<xs; y, > y2 > y3 > y* > y5
Funkcję f nazywamy malejącą, jeśli dla każdych x„x2eD, zachodzi:
x,<x2 => f(x,)>f(x2) x,>x2 => f(x,)<f(x2).
* Funkcja liniowa f(x)=ax jest malejgca dla a<0.
Wyszukiwarka
Podobne podstrony:
10478250?1689389228465s73544355843340941 o X1 X2 X3 X4 FT-13 FT-14 FT-15 V1 V2 V3 FT-16 FT-17 V4 V5
Untitled Scanned 26 - 52 - y - ♦. x2 + x3 • x4 = X1 + x2 + x3 • x4 = - *! + *2 + x
3. Malejąca X1,X2 c A, XI < X2, f(xl) > f(X2) 4. Nierosnąca XI,X2 e A, XI < X2, f(xl) ;>
292 293 o 292 5.14. TO = X1 + X5 Y1 = X4 + 25 Y2 = X3 + 24 Y3 = X2
HPIM5371 PROCES ODWRACALNY STAN POCZĄTKOWY STAN KOŃCOWY X1# X2,X3... &
7. Rozważmy zmienne Y, XI, X2, X3, X4, X5, X6. Wiadomo, że Xl=2+X4, X4=2X5. Który
Untitled 38 76 11A / . \ , <h *»a zmst = xl x2 x3 x4 x5 x6 x7 x8 x9 xlO /lin_pn/el_linii4/Integ
dd (22) 41 41 = o (4.10) a(x 1 + x2 + x3 + x4) + 6(1 + 1 +1 + 1) - &nbs
zadanie Niech U — {(x1.x2.x3) 6 IR3 : xi + 2x2 + 3x3 — 0} i niechw = (1,0,1). © a) U jest podprzestr
img428 (3) Podobnie lim (x4 - 3x2 + x -1) = lim X—>+oo X—>+oo X2 X3 X4 = +00
Jerzy Wasiluk, Aleksander Ostanin A B c D E ■■ F 1 2 X1 X2 X3 Wyrazy
Blaupunkt DMS bmp Blmipunkt (DMS x1, x2, x3,104,105)-Złącze ISO C10 czyli modele RDM i ROM 42, 82, 4
y = (*! + x2 + x3) * (x4 + xa + x2) * (x3 + x4 + x3) * (x7 + x2) * (x3 + x4 + x3 + x2) y = (x3 + x2
więcej podobnych podstron