Untitled 38

76 11A / . \\ , <h *»a '

zmst =

xl

x2

x3

x4

x5

x6

x7

x8

x9

xlO

/lin_pn/el_linii4/Integrator /lin_pn/el_linii/Integrator /lin_pn/el_linii/Integrator1 /lin_pn/e l_lini.il / Integrator 1 /lin_pn/el_liniil/Integrator /lin_pn/el_linii2/Integrator1 /Iin_pn/el_linii2/Integrator /Iin_pn/el_linii3/Integrator1 /lin_pn/el_linii3/Integrator /lin_pn/el_linii4/Integrator1

wynika, że w kolejności są to następujące zmienne⁴¹: x3, x4, x6, x8, xlO.

Powinno to potwierdzić poniższe polecenie, zlecające pokazanie na przykład 40-go wiersza macierzy zmiennych stanu:

» x (1, : )

Columns 1 through 7

1.7982    1.9426    0.0631    0.0579

1.8898    0.0481    1.8459

Columns 8 through 10

W celu narysowania tworzymy nową macierz, na przykład o nazwie z, będącą pod-macierzą macierzy zawierającą tylko wybrane kolumny: z=x(:,[3,4,6,8,10j);

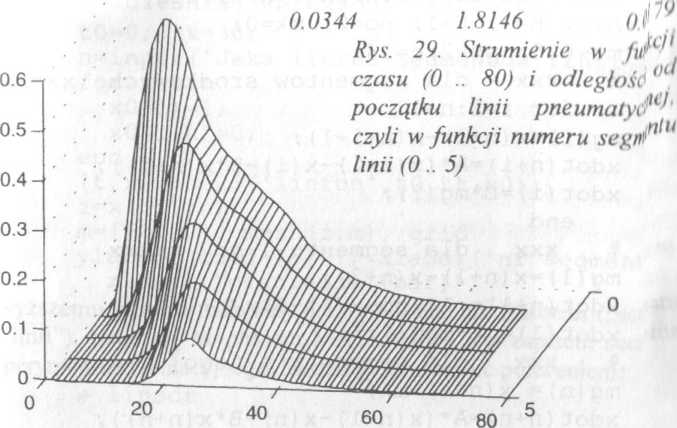
Graficzną reprezentację tej macierzy otrzymamy za pomocą poleceń: m=[100,201 mesh(z,m)

pokazaną na rysunlćU 29. Dwuelementowy wektor m deklaruje położenie rysunku w przestrzeni: azymut 130° i kat podniesienia 20°.

⁴¹ są to wyjścia z bloku Integrator 1 (Rys. 23) w kolejności: el linii, el linii I. el linii2, el Iinii3, el linii4 (Rys. 26)

6.3. Wariant 2: Tekstowe tworzenie modelu komputerov/⁹°

Teraz model utworzymy w postaci pliku tekstowego jako ^|Lin^ ^ MATLAETa. Symulację, to znaczy rozwiązanie równań różnic/}^0WV' zrealizujemy także za pomocą całkujących funkcji MATLAiłf’ ode23. Nie skorzystamy więc z bloków programowych SIMULINT ³ Krok 1: definiowanie modelu komputerowego w postaci rów/¹¹ " ^-niczkowych. Przyjmiemy następujące oznaczenia:

dpi dt	o	xdot(i)
dm, dt P,	>	xdot(n + i)
	t>	x(i)
^mi	>	x(n + i)
mgi	>	mg(i)