4544140648

Przykład zawartości pliku silnia.m zawierającego funkcje obliczającą wartość silnia:

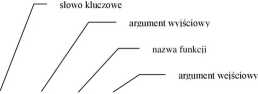
wiersz definicji funkcji wiersz H1 tekst pomocy

function y = silnia(x)

% Obliczanie wartości silnia % Funkcja silnia(n) zwraca wartość n!

% Wykorzystuje funkcję wbudowaną prod.    komentarz

y = prod (1 :x) ;    % Body    ciało funkcji

MATLAB przy pierwszym wywołaniu skryptu lub funkcji dokonuje jego kompilacji - dzięki temu każde następne użycie nie wymaga fazy interpretacji pliku. W przypadku dużych aplikacji można dokonać wstępnej kompilacji plików .m za pomocą funkcji pcode (powoduje to powstanie w bieżącym katalogu tzw. plików .p - preparsed). Taka kompilacja pozwala również na ukrycie kodu programu, ale jednocześnie ukrywa całą treść pomocy. Usunięcie skompilowanych funkcji z przestrzeni roboczej programu wykonuje się za pomocą polecenia elear functions.

1.7.3    Rodzaje funkcji

Z uwagi na sposób interpretacji można podzielić funkcje na następujące typy:

•    funkcje wbudowane - funkcje zdefiniowane wewnętrznie w MATLAB-ie. Jeżeli istnieją odpowiadające im pliki .ni (np. w folderach narzędziowych), to zawierają one jedynie teksty pomocy i wiersz wywołania funkcji wbudowanej,

•    funkcje pierwotne (główne) - podstawowy sposób użycia funkcji tworzonych przez użytkownika. Funkcja pierwotna jest pierwszą (i najczęściej jedyną) funkcją występującą w pliku .m. Uruchomienie takiej funkcji odbywa się przez wprowadzenie nazwy pliku w wierszu komendy -stąd najczęściej przyjmuje się, że nazwa funkcji tożsama jest z nazwą pliku,

•    podfunkcje (funkcje pomocnicze) - funkcje dodatkowo zdefiniowane wewnątrz pliku zawierającego definicję funkcji pierwotnej, wykorzystywane wewnątrz ciała funkcji pierwotnej. O ile funkcje pierwotne są dostępne z poza pliku, to do podfunkcji dostęp jest jedynie z wnętrza pliku. Każda funkcja rozpoczyna się wierszem definicji funkcji i posiada własny obszar danych. Poszczególne funkcje występują bezpośrednio jedna za drugą. Wszystkie definicje funkcji (lub żadna) zakończone są instrukcją end,

•    funkcje zagnieżdżone, definiowane wewnątrz definicji innych funkcji. Funkcje zagnieżdżone mogą sięgać do obszaru danych funkcji nadrzędnych. Każda z definicji funkcji zagnieżdżonej wewnątrz definicji innej funkcji musi kończyć się instrukcją end.

•    funkcje anonimowe - dają możliwość szybkiego definiowania funkcji na podstawie dowolnego wyrażenia MATLAB-a, bez tworzenia plików .m,

•    funkcje przeciążone - używane w przypadkach, gdy istnieje potrzeba tworzenia różnych funkcji dla różnych typów argumentów wejściowych, (podobnie jak w językach zorientowanych obiektowo),

•    funkcje prywatne - dają możliwość ograniczenia dostępu do funkcji (np. tylko w ramach klasy).

1.7.4    Uchwyty do funkcji

Użyteczna jest możliwość wprowadzenia zmiennej jako uchwytu do funkcji.Za przykład posłuży nam

zdefiniowanie procedury wyświetlającej wykres zadanej funkcji. Załóżmy, że w pliku o nazwie

plotFHandle.m umieszczono następujący tekst:

16