4734120223

Matematyczna

6€

www.omj.edu.pl

Kwadrat

Gazetka Olimpiady Matematycznej Juniorów

Nr 23

wrzesień 2019

IJSH23000TD8

C

iy%. 5

Zaginamy

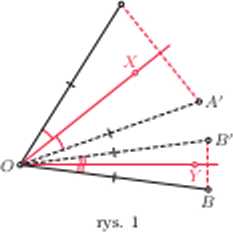
Rozpatrzmy odcinki OĄ OB o równej długości tworzące kąt o mierze o. wewnątrz którego znajduje się kąt X()Y o mierze 0. Ustalmy oznaczenia w taki sposób. by odcinki OA, OX. OY, OB hyły ustawione w tej właśnie kolejności wokół punktu O (rys. 1).

J<śli przez A\ B’ oznaczymy obrazy odpowiednio punktów A. B w symetriach względem prostych OX. OY. to wówczas OA = O A* oraz OB = OB' i w konsekwencji O A* =OB\ Ponadto, jeśli 20 to

4A'OB’ = 4XOY- {łXOA’ + ĄYO&) =

= 4XOY- [tXOA + 4YOB) =

= 0-{a-0)=20-a.

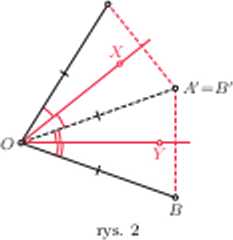
Z rachunku tego wynika w szczególności, że jeśli a = 20, to punkty A’ i B^f pokrywają się (r>s. 2).

A

Zobaczmy. Jak .zagięcie"* punktów A, B do wnętrza kipa XOY może pomóc w rozwiązaniu zadań.

Zadanie 1.

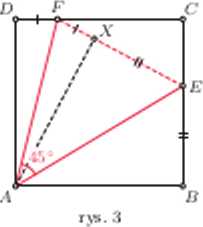
Dany jest kwadrat ABCD (rys. 3). Punkty E, F leżą odpowiednio na bokach BC, CD. przy czym ĄEAE = 45°. Udowodnij, że BE + DF = EF.

Rozwiązanie

W naszej konfiguracji rolę odcinków O A i OB pełnią odcinki AB i AD. tworzące kąt o mierze a =90°. Wewnątrz tego kąt a znajduje się kip EAF o mierze $=45°.

Odbijmy więc punkty B. D symetrycznie względem prostych AE. AE. uzyskując odpowiednio punkty B^f, IX. Ponieważ o =20, więc punkty IX i IX pokrywają się z pewnym punktem A'. Ponadto

łAXE+ łAXF = $ABE+ĄADF=Wf + 90*= 180°, 8kpi wniosek, że piuikt A' leż>* na odcinku EF. Zatem BE + DE = X E + X F = EF, co kończy rozwiązanie zadania.

Zadanie 2.

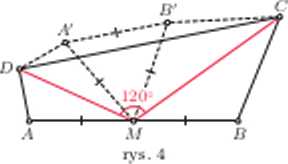
W czworokącie wypukłym ABCD punkt M jest środkiem hoku AB oraz $CMD = 120* (rys. 4). Udowodnij, że DA + ±AB+ BC> DC.

Rozwiązanie

Rolę odcinków O A i OB pełnią teraz odcinki AJ A i MB wyznaczające kąt o = ISO*. Wewnątrz tego kipa znajduje się kip CM D o mierze 0= 120°.

Odbijmy zatem punkty A. B symetiycznie kolejno względem prostych DM. CM. uzyskując odpowiednio punkty A’. li. Wówczas MA’ =M li oraz

łJtM li = 20-o = 240° -180° = 00°.

Wobec tego trójkąt M MB* jest równoboczny. W szczególności A^fli = M A' = MA = ±AB. W związku z tym DA + $AB + BC = DA' + A^fB^f + B'C > DC. co kończy dowód.

Zadanie 3.

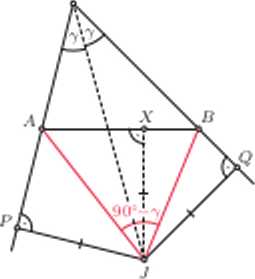
Dany jest trójkąt ABC. w którym %ACB = 2y. Punkt ./ leży na dwusiecznej kpa ACB oraz na ze-wnątrz tiójkąta ABC, przy czym spełniony jest warunek 4AJB = Wf-y.

Wykaż, że punkt ./ leży na dwusiecznych kątów zewnętrznych trójkąta ABC przy wierzchołkach A i B.

Rozwiązanie

Oznaczmy przez P i Q rzuty prostokątne punktu ./ odpowiednio na proste AC i BC (ryB. 5). Ponadto 4AJC< <AJB = W -y, skipi wynika, że ĄCAJ = 180° - <fACJ - ŹAJC >

> 180°-y-(90°-y) = 90°.

Podobnie, ŹCBJ >90*. St.pl wniosek, że punkty P i Q leżą na przedłużeniach boków AC i BC.

iu 1 Fundacja

u

MINISTERSTWO

EDUKACJI

NARODOWEJ

. c StMirzyszeiM

Otanptada Matematyczna Juniorów jest wspórtnansowana ze środków krajowych Mnteterstwa Edukaqi Narodowej

OWnptadę doinansowiąe Fundaqa mBanku